Previous Page

|

Next Page

The Working Basis Matrix

Let be the basis matrix of NPSC. The following partitioning is done:

where

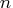• is the number of nodes.
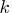• is the number of side constraints.
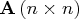• is the network component of the basis. Most of the columns of this matrix are columns of the problem's node-arc incidence matrix. The arcs associated with columns of 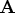, called key basic variables or key arcs, form a spanning tree. The data structures of the spanning tree of this submatrix of the basis 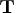enable the computations involving 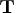and the manner in which 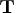is updated to be very efficient, especially those dealing with 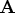(or ).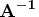
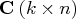• are the key arcs' side constraint coefficient columns.
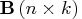• are the node-arc incidence matrix columns of the nontree arcs. The columns of 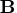having nonzero elements are associated with basic nonspanning tree arcs.
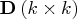• are the constraint coefficient columns of nonkey basic variables. Nonkey basic variables not only include nontree basic arcs but also basic slack, surplus, artificial, or nonarc variables.

It is more convenient to factor by block triangular matrices and , such that . The matrices and are used instead of because they are less burdensome to work with. You can perform block substitution when solving the simplex iteration linear systems of equations

where and is called the working basis matrix.

To perform block substitution, you need the tree data structure of the matrix, and also the , , and matrices. Because the matrix consists of columns of the constraint coefficient matrix, the maintenance of from iteration to iteration simply entails changing information specifying which columns of the constraint coefficient matrix compose .

The matrix is usually very sparse. Fortunately, the information in can be initialized easily using the tree structures. In most iterations, only one column is replaced by a new one. The values of the elements of the new column may already be known from preceding steps of the simplex iteration.

The working basis matrix is the submatrix that presents the most computational complexity. However, PROC NETFLOW usually can use classical simplex pivot techniques. In many iterations, only one column of changes. Sometimes it is not necessary to update or its inverse at all.

If INVD_2D is specified in the PROC NETFLOW statement, only one row and one column may need to be changed in the before the next simplex iteration can begin. The new contents of the changed column are already known. The new elements of the row that changes are influenced by the contents of a row of that is very sparse.

If INVD_2D is not specified in the PROC NETFLOW statement, the Bartels-Golub update can be used to update the LU factors of . The choice must be made whether to perform a series of updates (how many depends on the number of nonzeros in a row of ), or refactorization.