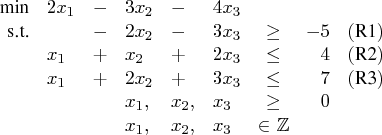The Mixed Integer Linear Programming Solver

Getting Started

The following example illustrates how you can use the OPTMODEL procedure to solve mixed integer linear programs. For more examples, see the section "Examples". Suppose you want to solve the following problem:

${min} & 2x_1 & - & 3x_2 & - & 4x_3 & & & \ {s.t.} & & - & 2x_2 & - & 3x_3 & \ge... ...1, & x_2, & x_3 & \geq & 0 & \ & & & x_1, & x_2, & x_3 & \in \mathbb{z} & & \$

You can use the following code to call the OPTMODEL procedure for solving mixed integer linear programs:

    proc optmodel;
       var x{1..3} >= 0 integer;
    
       min f = 2*x[1] - 3*x[2] - 4*x[3];
    
       con r1: -2*x[2] - 3*x[3] >= -5;
       con r2: x[1] + x[2] + 2*x[3] <= 4;
       con r3: x[1] + 2*x[2] + 3*x[3] <= 7;
    
       solve with milp / presolver = automatic heuristics = automatic;
       print x;
    quit;

The PRESOLVER= and HEURISTICS= options specify the levels for presolving and applying heuristics, respectively. In this example, each option is set to its default value, AUTOMATIC, meaning that the solver determines the appropriate levels for presolve and heuristics automatically.

The optimal value of x is shown in Output 9.1.

The OPTMODEL Procedure

[1]	x
1	0
2	1
3	1

Figure 9.1: Solution Output

The solution summary stored in the macro variable _OROPTMODEL_ can be viewed by issuing the following statement:

  
  
    %put &_OROPTMODEL_;

This produces the output shown in Output 9.2.

                                                                                
                                                                                 
                                                                                 
 STATUS=OK SOLUTION_STATUS=OPTIMAL OBJECTIVE=-7 RELATIVE_GAP=0 ABSOLUTE_GAP=0 PRI
 MAL_INFEASIBILITY=0 BOUND_INFEASIBILITY=0 INTEGER_INFEASIBILITY=0 BEST_BOUND=. N
 ODES=1 ITERATIONS=2 PRESOLVE_TIME=0.00 SOLUTION_TIME=0.00

Figure 9.2: Macro Output

Top of Page