The Linear Programming Solver: LP Solver Options :: SAS/OR(R) 9.2 User's Guide: Mathematical Programming

The Linear Programming Solver

LP Solver Options

This section describes the options recognized by the LP solver. These options can be specified after a forward slash (/) in the SOLVE statement, provided that the LP solver is explicitly specified using a WITH clause.

If the LP solver terminates before reaching an optimal solution, an intermediate solution is available. You can access this solution by using the .sol variable suffix in the OPTMODEL procedure. See the section "Suffixes" for details.

Solver Options

IIS=OFF(0) ON(1) (experimental)

specifies whether the LP solver performs detection of an irreducible infeasible set (IIS). When IIS=ON, the LP solver tries to identify a set of constraints and variables that form an IIS. If an IIS is found, information about the infeasibilities can be found in the .status values of the constraints and variables. If no IIS is detected, then a solver is called to continue solving the problem. The default value of this option is OFF. The OPTMODEL option PRESOLVER=NONE should be specified when IIS=ON is specified; otherwise, the IIS results can be incomplete. See the section "Irreducible Infeasible Set" for details about the IIS= option. See "Suffixes" for details about the .status suffix.

SOLVER=option

specifies one of the following LP solvers:

Option	Description
PRIMAL (PS)	Use primal simplex solver.
DUAL (DS)	Use dual simplex solver.
ITERATIVE (II), experimental	Use interior point solver.

The valid abbreviated value for each option is indicated in parentheses. By default, the dual simplex solver is used.

Presolve Options

PRESOLVER=option

specifies one of the following presolve options:

Option	Description
NONE (0)	Disable presolver.
AUTOMATIC (-1)	Apply presolver by using default setting.
BASIC (1)	Perform basic presolve like removing empty rows, columns, and fixed variables.
MODERATE (2)	Perform basic presolve and apply other inexpensive presolve techniques.
AGGRESSIVE (3)	Perform moderate presolve and apply other aggressive (but expensive) presolve techniques.

The default option is AUTOMATIC. See the section "Presolve" for details.

Control Options

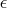
FEASTOL= $\epsilon$

specifies the feasibility tolerance, 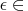$\epsilon \in$ [1E - 9, 1E - 4], for determining the feasibility of a variable. The default value is 1E - 6.

MAXITER=

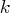
specifies the maximum number of iterations. The value

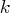can be any integer between one and the largest four-byte signed integer, which is 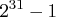$2^{31} - 1$ . If you do not specify this option, the procedure does not stop based on the number of iterations performed.

MAXTIME=

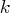
specifies an upper limit of

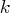seconds of time for the optimization process. The timer used by this option is determined by the value of the TIMETYPE= option. If you do not specify this option, the procedure does not stop based on the amount of time elapsed.

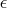
OPTTOL= $\epsilon$

specifies the optimality tolerance, 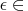$\epsilon \in$ [1E - 9, 1E - 4], for declaring optimality. The default value is 1E - 6.

PRINTFREQ=

specifies that the printing of the solution progress to the iteration log is to occur after every

iterations. The print frequency,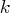

, is an integer between zero and the largest four-byte signed integer, which is $2^{31} - 1$ .

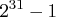The value 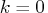disables the printing of the progress of the solution. If the simplex algorithms are used, the default value of this option is determined dynamically according to the problem size. If the interior point algorithm is used, the default value of this option is 1.

TIMETYPE=CPU(0) REAL(1)

sets the timer used by the MAXTIME= option, and controls the type of time reported by PRESOLVE_TIME and SOLUTION_TIME in the _OROPTMODEL_ macro variable. The "Optimization Statistics" table, an output of PROC OPTMODEL if option PRINTLEVEL=2 is specified in the PROC OPTMODEL statement, also includes the same time values for "Presolver Time" and "Solver Time." The other times (such as "Problem Generation Time") in this table are always CPU times. The default value of this option is CPU.

Simplex Algorithm Options

BASIS=option

specifies the following options for generating an initial basis:

Option	Description
CRASH (0)	Generate an initial basis by using crash techniques (Maros 2003). The procedure creates a triangular basic matrix consisting of both decision variables and slack variables.
SLACK (1)	Generate an initial basis by using all slack variables.
WARMSTART (2)	Start the simplex solvers with available basis.

The default option for the primal simplex solver is CRASH (0). The default option for the dual simplex solver is SLACK(1).

PRICETYPE=option

specifies one of the following pricing strategies for the simplex solvers:

Option	Description
HYBRID (0)	Use hybrid Devex and steepest-edge pricing strategies. Available for primal simplex solver only.
PARTIAL (1)	Use partial pricing strategy. Optionally, you can specify QUEUESIZE=. Available for primal simplex solver only.
FULL (2)	Use the most negative reduced cost pricing strategy.
DEVEX (3)	Use Devex pricing strategy.
STEEPESTEDGE (4)	Use steepest-edge pricing strategy.

The default pricing strategy for the primal simplex solver is HYBRID and that for the dual simplex solver is STEEPESTEDGE. See the section "Pricing Strategies for the Primal Simplex Solver" for details.

QUEUESIZE=

specifies the queue size, $k\in[1, n]$ , where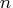

is the number of decision variables. This queue is used for finding an entering variable in the simplex iteration. The default value is chosen adaptively based on the number of decision variables. This option is used only when PRICETYPE=PARTIAL.

SCALE=option

specifies one of the following scaling options:

Option	Description
NONE (0)	Disable scaling.
AUTOMATIC (-1)	Automatically apply scaling procedure if necessary.

The default option is AUTOMATIC.

Interior Point Algorithm Options

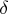
STOP_DG= $\delta$: specifies the desired relative duality gap, 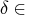$\delta \in$ [1E - 9, 1E - 4]. This is the relative difference between the primal and dual objective function values and is the primary solution quality parameter. The default value is 1E - 6. See the section "The Interior Point Algorithm: Overview" for details.
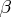
STOP_DI= $\beta$: specifies the maximum allowed relative dual constraints violation, 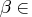$\beta \in$ [1E - 9, 1E - 4]. The default value is 1E - 6. See the section "The Interior Point Algorithm: Overview" for details.
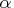
STOP_PI= $\alpha$: specifies the maximum allowed relative bound and primal constraints violation, 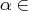$\alpha \in$ [1E - 9, 1E - 4]. The default value is 1E - 6. See the section "The Interior Point Algorithm: Overview" for details.

Top of Page