| The NLPC Nonlinear Optimization Solver |
NLPC Solver Options
This section describes the options recognized by the NLPC solver. These options can be specified after a forward slash (/) in the SOLVE statement, provided that the NLPC solver is explicitly specified using a WITH clause.
The following notation is used in this section and the section "Details":
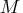
- a nonnegative floating-point number
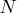
- a nonnegative integer
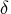
- a small nonnegative floating-point number
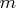
- number of general nonlinear constraints, including the linear constraints but not the bound constraints
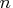
- dimension of
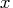 , i.e., the number of decision variables
, i.e., the number of decision variables
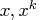
- iterate, i.e., the vector of
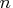 decision variables;
decision variables; 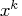 denotes
the iterate at the
denotes
the iterate at the 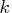 th iteration.
th iteration.
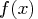
- objective function
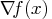
- gradient of the objective function
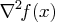
- Hessian of the objective function
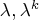
- Lagrange multiplier vector,
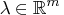 ;
;
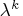 denotes the estimate of the Lagrange multipliers at the
denotes the estimate of the Lagrange multipliers at the 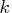 th
iteration
th
iteration
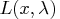
- Lagrangian function of constrained problems
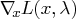
- gradient of the Lagrangian function with respect to
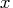
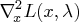
- Hessian of the Lagrangian function with respect
to
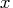
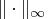
- infinity norm of a vector; for example,
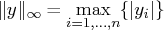 for
for 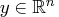
-
ABSOPTTOL=
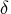
-
specifies the tolerance for the absolute optimality error. For the solver to terminate,
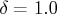 E-3 for all four
optimization techniques. The range of valid values for
E-3 for all four
optimization techniques. The range of valid values for 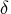 is between and 1.
is between and 1.
Note: For more information about this termination criterion, see the section "Optimality Control".
-
MAXFUNC=
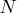
- MAXFEVAL=
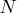
-
specifies that the optimization process stop after a maximum of
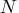 function calls. The value of
function calls. The value of 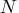 can be no larger than the largest
four-byte signed integer, which is
can be no larger than the largest
four-byte signed integer, which is 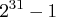 . The default values of
. The default values of
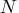 are as follows:
are as follows:
- for TECH=TRUREG or NEWTYP,
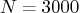
- for TECH=QUANEW,
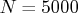
- for TECH=CONGRA,
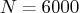
- for TECH=TRUREG or NEWTYP,
-
MAXITER=
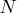
-
specifies that the optimization process stop after a maximum of
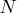 iterations. The value of
iterations. The value of 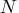 can be no larger than the largest
four-byte signed integer, which is
can be no larger than the largest
four-byte signed integer, which is 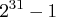 . The default values
of
. The default values
of 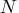 are as follows:
are as follows:
- for TECH=TRUREG or NEWTYP,
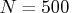
- for TECH=QUANEW,
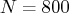
- for TECH=CONGRA,

- for TECH=TRUREG or NEWTYP,
-
MAXTIME=
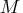
-
specifies an upper limit of
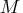 seconds of real time for the optimization process.
If you do not specify this option, the optimization process does not stop based on the amount
of time elapsed. Note that the time specified by the MAXTIME= option is checked only at
the end of each iteration. The optimization terminates when the actual running time is
greater than or equal to
seconds of real time for the optimization process.
If you do not specify this option, the optimization process does not stop based on the amount
of time elapsed. Note that the time specified by the MAXTIME= option is checked only at
the end of each iteration. The optimization terminates when the actual running time is
greater than or equal to 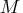 .
. -
OBJLIMIT=
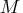
-
specifies an upper limit on the magnitude of the objective value. For a minimization
problem, the algorithm terminates when the objective value becomes less than
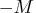 ; for a
maximization problem, the algorithm stops when the objective value exceeds
; for a
maximization problem, the algorithm stops when the objective value exceeds 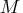 . When
this happens, it implies that either the problem is unbounded or the algorithm diverges.
If optimization were allowed to continue, numerical difficulty might be encountered. The
default value is
. When
this happens, it implies that either the problem is unbounded or the algorithm diverges.
If optimization were allowed to continue, numerical difficulty might be encountered. The
default value is 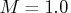 E
E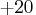 . The range of valid values for
. The range of valid values for 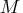 is
is  E
E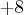 .
. -
PRINTFREQ=
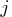
-
specifies that the printing of the solution progress to the iteration log should occur
after every
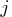 iterations. The print frequency,
iterations. The print frequency, 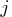 , is an integer between zero and
the largest four-byte signed integer, which is
, is an integer between zero and
the largest four-byte signed integer, which is 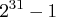 . The value
. The value
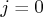 disables the printing of the progress of the solution.
Note that iteration and the last iteration are always displayed for
disables the printing of the progress of the solution.
Note that iteration and the last iteration are always displayed for 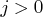 .
.By default, the NLPC solver does not display the iteration log.
-
RELOPTTOL=
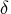
-
specifies the tolerance for the relative optimality error. For the solver to terminate,
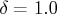 E-6 for all four
optimization techniques. The range of valid values for
E-6 for all four
optimization techniques. The range of valid values for 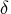 is between and 1.
is between and 1.
Note: For more information about this termination criterion, see the section "Optimality Control".
- TECH=keyword
- TECHNIQUE=keyword
- SOLVER=keyword
-
specifies the optimization technique. Valid keywords are as follows:
- CONGRA or CGR
uses a conjugate gradient method. - NEWTYP or NTY
uses a Newton-type method with line search. - TRUREG or TRE
uses a trust region method. - QUANEW or QNE (experimental)
uses a quasi-Newton method with the BFGS update. QUANEW is the optimization technique in the NLPC solver to solve problems with nonlinear constraints.
The default technique is CONGRA if there are more than 1000 variables in the problem (possibly presolved) and TRUREG otherwise. See the section "Presolver" for details about presolver.
- CONGRA or CGR
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.