The INTPOINT Procedure
-
Overview

-
Getting Started

-
Syntax
 Functional SummaryDictionary of OptionsPROC INTPOINT StatementCAPACITY StatementCOEF StatementCOLUMN StatementCOST StatementDEMAND StatementHEADNODE StatementID StatementLO StatementNAME StatementNODE StatementQUIT StatementRHS StatementROW StatementRUN StatementSUPDEM StatementSUPPLY StatementTAILNODE StatementTYPE StatementVAR Statement
Functional SummaryDictionary of OptionsPROC INTPOINT StatementCAPACITY StatementCOEF StatementCOLUMN StatementCOST StatementDEMAND StatementHEADNODE StatementID StatementLO StatementNAME StatementNODE StatementQUIT StatementRHS StatementROW StatementRUN StatementSUPDEM StatementSUPPLY StatementTAILNODE StatementTYPE StatementVAR Statement -
Details
 Input Data SetsOutput Data SetsConverting Any PROC INTPOINT Format to an MPS-Format SAS Data SetCase SensitivityLoop ArcsMultiple ArcsFlow and Value BoundsTightening Bounds and Side ConstraintsReasons for InfeasibilityMissing S Supply and Missing D Demand ValuesBalancing Total Supply and Total DemandHow to Make the Data Read of PROC INTPOINT More EfficientStopping Criteria
Input Data SetsOutput Data SetsConverting Any PROC INTPOINT Format to an MPS-Format SAS Data SetCase SensitivityLoop ArcsMultiple ArcsFlow and Value BoundsTightening Bounds and Side ConstraintsReasons for InfeasibilityMissing S Supply and Missing D Demand ValuesBalancing Total Supply and Total DemandHow to Make the Data Read of PROC INTPOINT More EfficientStopping Criteria -
Examples
 Production, Inventory, Distribution ProblemAltering Arc DataAdding Side ConstraintsUsing Constraints and More Alteration to Arc DataNonarc Variables in the Side ConstraintsSolving an LP Problem with Data in MPS FormatConverting to an MPS-Format SAS Data SetMigration to OPTMODEL: Production, Inventory, Distribution
Production, Inventory, Distribution ProblemAltering Arc DataAdding Side ConstraintsUsing Constraints and More Alteration to Arc DataNonarc Variables in the Side ConstraintsSolving an LP Problem with Data in MPS FormatConverting to an MPS-Format SAS Data SetMigration to OPTMODEL: Production, Inventory, Distribution - References
Mathematical Description of LP
A linear programming (LP) problem has a linear objective function and a collection of linear constraints. PROC INTPOINT finds the values of variables that minimize the total cost of the solution. The value of each variable is on or between the variable’s lower and upper bounds, and the constraints are satisfied.
If an LP has g variables and k constraints, then the formal statement of the problem solved by PROC INTPOINT is
![\[ \begin{array}{ll} \mr{minimize} & d^ T z \\ \mr{subject\ to} & Q z \, \{ \geq , =, \leq \} \, r \\ & m \leq z \leq v \\ \end{array} \]](images/ormplpug_intpoint0019.png)
where
-
z is the
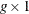 variable value vector
variable value vector
-
Q is the
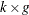 constraint coefficient matrix for the variables, where
constraint coefficient matrix for the variables, where 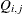 is the coefficient of variable j in the ith constraint
is the coefficient of variable j in the ith constraint
-
r is the
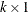 side constraint right-hand-side vector
side constraint right-hand-side vector
-
m is the
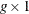 variable lower bound vector
variable lower bound vector
-
v is the
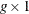 variable upper bound vector
variable upper bound vector