The NLP Procedure
- Overview
-
Getting Started

-
Syntax
 Functional SummaryDictionary of OptionsPROC NLP StatementARRAY StatementBOUNDS StatementBY StatementCRPJAC StatementDECVAR StatementGRADIENT StatementHESSIAN StatementINCLUDE StatementJACNLC StatementJACOBIAN StatementLABEL StatementLINCON StatementMATRIX StatementMIN, MAX, and LSQ StatementsMINQUAD and MAXQUAD StatementsNLINCON StatementPROFILE StatementProgram Statements
Functional SummaryDictionary of OptionsPROC NLP StatementARRAY StatementBOUNDS StatementBY StatementCRPJAC StatementDECVAR StatementGRADIENT StatementHESSIAN StatementINCLUDE StatementJACNLC StatementJACOBIAN StatementLABEL StatementLINCON StatementMATRIX StatementMIN, MAX, and LSQ StatementsMINQUAD and MAXQUAD StatementsNLINCON StatementPROFILE StatementProgram Statements -
Details
 Criteria for OptimalityOptimization AlgorithmsFinite-Difference Approximations of DerivativesHessian and CRP Jacobian ScalingTesting the Gradient SpecificationTermination CriteriaActive Set MethodsFeasible Starting PointLine-Search MethodsRestricting the Step LengthComputational ProblemsCovariance MatrixInput and Output Data SetsDisplayed OutputMissing ValuesComputational ResourcesMemory LimitRewriting NLP Models for PROC OPTMODEL
Criteria for OptimalityOptimization AlgorithmsFinite-Difference Approximations of DerivativesHessian and CRP Jacobian ScalingTesting the Gradient SpecificationTermination CriteriaActive Set MethodsFeasible Starting PointLine-Search MethodsRestricting the Step LengthComputational ProblemsCovariance MatrixInput and Output Data SetsDisplayed OutputMissing ValuesComputational ResourcesMemory LimitRewriting NLP Models for PROC OPTMODEL -
Examples

- References
The following introductory examples illustrate how to get started using the NLP procedure.
Consider the simple example of minimizing the Rosenbrock function (Rosenbrock 1960):
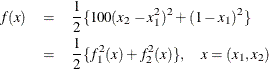
The minimum function value is ![]() at
at ![]() . This problem does not have any constraints.
. This problem does not have any constraints.
The following statements can be used to solve this problem:
proc nlp; min f; decvar x1 x2; f1 = 10 * (x2 - x1 * x1); f2 = 1 - x1; f = .5 * (f1 * f1 + f2 * f2); run;
The MIN
statement identifies the symbol f that characterizes the objective function in terms of f1 and f2, and the DECVAR
statement names the decision variables x1 and x2. Because there is no explicit optimizing algorithm option specified (TECH=
), PROC NLP uses the Newton-Raphson method with ridging, the default algorithm when there are no constraints.
A better way to solve this problem is to take advantage of the fact that f is a sum of squares of ![]() and
and ![]() and to treat it as a least squares problem. Using the LSQ
statement instead of the MIN
statement tells the procedure that this is a least squares problem, which results in the use of one of the specialized algorithms
for solving least squares problems (for example, Levenberg-Marquardt).
and to treat it as a least squares problem. Using the LSQ
statement instead of the MIN
statement tells the procedure that this is a least squares problem, which results in the use of one of the specialized algorithms
for solving least squares problems (for example, Levenberg-Marquardt).
proc nlp; lsq f1 f2; decvar x1 x2; f1 = 10 * (x2 - x1 * x1); f2 = 1 - x1; run;
The LSQ statement results in the minimization of a function that is the sum of squares of functions that appear in the LSQ statement. The least squares specification is preferred because it enables the procedure to exploit the structure in the problem for numerical stability and performance.
PROC NLP displays the iteration history and the solution to this least squares problem as shown in Figure 7.1. It shows that the solution has ![]() and
and ![]() . As expected in an unconstrained problem, the gradient at the solution is very close to 0.
. As expected in an unconstrained problem, the gradient at the solution is very close to 0.
Bounds on the decision variables can be used. Suppose, for example, that it is necessary to constrain the decision variables in the previous example to be less than 0.5. That can be done by adding a BOUNDS statement.
proc nlp; lsq f1 f2; decvar x1 x2; bounds x1-x2 <= .5; f1 = 10 * (x2 - x1 * x1); f2 = 1 - x1; run;
The solution in Figure 7.2 shows that the decision variables meet the constraint bounds.
More general linear equality or inequality constraints of the form
can be specified in a LINCON
statement. For example, suppose that in addition to the bounds constraints on the decision variables it is necessary to guarantee
that the sum ![]() is less than or equal to 0.6. That can be achieved by adding a LINCON
statement:
is less than or equal to 0.6. That can be achieved by adding a LINCON
statement:
proc nlp; lsq f1 f2; decvar x1 x2; bounds x1-x2 <= .5; lincon x1 + x2 <= .6; f1 = 10 * (x2 - x1 * x1); f2 = 1 - x1; run;
The output in Figure 7.3 displays the iteration history and the convergence criterion.
Figure 7.3: Least Squares with Bounds and Linear Constraints Iteration History
| Iteration | Restarts | Function Calls |
Active Constraints |
Objective Function |
Objective Function Change |
Max Abs Gradient Element |
Lambda | Ratio Between Actual and Predicted Change |
||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 5 | 0 | ' | 0.16789 | 0.1775 | 0.4576 | 166.9 | 0.522 | |
| 2 | 1 | 7 | 1 | 0.16672 | 0.00117 | 0.2190 | 0.00471 | 0.0117 | ||
| 3 | 1 | 8 | 1 | 0.16658 | 0.000140 | 0.000508 | 0 | 0.998 | ||
| 4 | 1 | 9 | 1 | 0.16658 | 7.52E-10 | 9.253E-7 | 0 | 0.998 |
Figure 7.4 shows that the solution satisfies the linear constraint. Note that the procedure displays the active constraints (the constraints that are tight) at optimality.
More general nonlinear equality or inequality constraints can be specified using an NLINCON statement. Consider the least squares problem with the additional constraint
This constraint is specified by a new function c1 constrained to be greater than or equal to 0 in the NLINCON
statement. The function c1 is defined in the programming statements.
proc nlp tech=QUANEW; min f; decvar x1 x2; bounds x1-x2 <= .5; lincon x1 + x2 <= .6; nlincon c1 >= 0; c1 = x1 * x1 - 2 * x2; f1 = 10 * (x2 - x1 * x1); f2 = 1 - x1; f = .5 * (f1 * f1 + f2 * f2); run;
Figure 7.5 shows the iteration history, and Figure 7.6 shows the solution to this problem.
Figure 7.5: Least Squares with Bounds, Linear and Nonlinear Constraints, Iteration History
| Dual Quasi-Newton Optimization |
| Modified VMCWD Algorithm of Powell (1978, 1982) |
| Dual Broyden - Fletcher - Goldfarb - Shanno Update (DBFGS) |
| Lagrange Multiplier Update of Powell(1982) |
| Parameter Estimates | 2 |
|---|---|
| Lower Bounds | 0 |
| Upper Bounds | 2 |
| Linear Constraints | 1 |
| Nonlinear Constraints | 1 |
| Iteration | Restarts | Function Calls |
Objective Function |
Maximum Constraint Violation |
Predicted Function Reduction |
Step Size |
Maximum Gradient Element of the Lagrange Function |
|
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 9 | 1.21827 | 0 | 0.8823 | 0.437 | 5.845 | |
| 2 | 0 | 10 | 0.78787 | 0 | 0.5262 | 1.000 | 2.616 | |
| 3 | 0 | 12 | 0.72214 | 0 | 0.2500 | 0.147 | 2.849 | |
| 4 | 0 | 13 | 0.55450 | 0 | 0.1977 | 1.000 | 2.509 | |
| 5 | 0 | 14 | 0.42378 | 0 | 0.2537 | 1.000 | 0.789 | |
| 6 | 0 | 16 | 0.39842 | 0 | 0.1574 | 0.114 | 0.760 | |
| 7 | 0 | 18 | 0.35979 | 0 | 0.0649 | 0.366 | 0.320 | |
| 8 | 0 | 19 | 0.35429 | 0 | 0.0548 | 1.000 | 1.683 | |
| 9 | 0 | 20 | 0.33415 | 0 | 0.00758 | 1.000 | 0.119 | |
| 10 | 0 | 21 | 0.33026 | 0 | 0.000455 | 1.000 | 0.121 | |
| 11 | 0 | 22 | 0.33005 | 0 | 0.000044 | 1.000 | 0.00221 | |
| 12 | 0 | 23 | 0.33003 | 0 | 5.683E-8 | 1.000 | 0.00012 |
| Optimization Results | |||
|---|---|---|---|
| Iterations | 12 | Function Calls | 24 |
| Gradient Calls | 15 | Active Constraints | 0 |
| Objective Function | 0.330030744 | Maximum Constraint Violation | 0 |
| Maximum Projected Gradient | 3.0494342639 | Value Lagrange Function | 0.330030744 |
| Maximum Gradient of the Lagran Func | 3.0494342639 | Slope of Search Direction | -5.683122E-8 |
Not all of the optimization methods support nonlinear constraints. In particular the Levenberg-Marquardt method, the default for LSQ, does not support nonlinear constraints. (For more information about the particular algorithms, see the section Optimization Algorithms.) The Quasi-Newton method is the prime choice for solving nonlinear programs with nonlinear constraints. The option TECH= QUANEW in the PROC NLP statement causes the Quasi-Newton method to be used.
The following is a very simple example of a maximum likelihood estimation problem with the log likelihood function:
The maximum likelihood estimates of the parameters ![]() and
and ![]() form the solution to
form the solution to
where
In the following DATA step, values for x are input into SAS data set X; this data set provides the values of ![]() .
.
data x; input x @@; datalines; 1 3 4 5 7 ;
In the following statements, the DATA=
X specification drives the building of the objective function. When each observation in the DATA=
X data set is read, a new term ![]() using the value of
using the value of ![]() is added to the objective function LOGLIK specified in the MAX
statement.
is added to the objective function LOGLIK specified in the MAX
statement.
proc nlp data=x vardef=n covariance=h pcov phes; profile mean sigma / alpha=.5 .1 .05 .01; max loglik; parms mean=0, sigma=1; bounds sigma > 1e-12; loglik=-0.5*((x-mean)/sigma)**2-log(sigma); run;
After a few iterations of the default Newton-Raphson optimization algorithm, PROC NLP produces the results shown in Figure 7.7.
In unconstrained maximization, the gradient (that is, the vector of first derivatives) at the solution must be very close to zero and the Hessian matrix at the solution (that is, the matrix of second derivatives) must have nonpositive eigenvalues. The Hessian matrix is displayed in Figure 7.8.
Under reasonable assumptions, the approximate standard errors of the estimates are the square roots of the diagonal elements of the covariance matrix of the parameter estimates, which (because of the COV= H specification) is the same as the inverse of the Hessian matrix. The covariance matrix is shown in Figure 7.9.
The PROFILE statement computes the values of the profile likelihood confidence limits on SIGMA and MEAN, as shown in Figure 7.10.
Figure 7.10: Confidence Limits
| Wald and PL Confidence Limits | |||||||
|---|---|---|---|---|---|---|---|
| N | Parameter | Estimate | Alpha | Profile Likelihood Confidence Limits |
Wald Confidence Limits | ||
| 1 | mean | 4.000000 | 0.500000 | 3.384431 | 4.615569 | 3.396718 | 4.603282 |
| 1 | mean | . | 0.100000 | 2.305716 | 5.694284 | 2.528798 | 5.471202 |
| 1 | mean | . | 0.050000 | 1.849538 | 6.150462 | 2.246955 | 5.753045 |
| 1 | mean | . | 0.010000 | 0.670351 | 7.329649 | 1.696108 | 6.303892 |
| 2 | sigma | 2.000000 | 0.500000 | 1.638972 | 2.516078 | 1.573415 | 2.426585 |
| 2 | sigma | . | 0.100000 | 1.283506 | 3.748633 | 0.959703 | 3.040297 |
| 2 | sigma | . | 0.050000 | 1.195936 | 4.358321 | 0.760410 | 3.239590 |
| 2 | sigma | . | 0.010000 | 1.052584 | 6.064107 | 0.370903 | 3.629097 |