The NLP Procedure
- Overview
-
Getting Started
-
SyntaxFunctional SummaryDictionary of OptionsPROC NLP StatementARRAY StatementBOUNDS StatementBY StatementCRPJAC StatementDECVAR StatementGRADIENT StatementHESSIAN StatementINCLUDE StatementJACNLC StatementJACOBIAN StatementLABEL StatementLINCON StatementMATRIX StatementMIN, MAX, and LSQ StatementsMINQUAD and MAXQUAD StatementsNLINCON StatementPROFILE StatementProgram Statements
-
DetailsCriteria for OptimalityOptimization AlgorithmsFinite-Difference Approximations of DerivativesHessian and CRP Jacobian ScalingTesting the Gradient SpecificationTermination CriteriaActive Set MethodsFeasible Starting PointLine-Search MethodsRestricting the Step LengthComputational ProblemsCovariance MatrixInput and Output Data SetsDisplayed OutputMissing ValuesComputational ResourcesMemory LimitRewriting NLP Models for PROC OPTMODEL
-
Examples
- References
Two algorithms are used to obtain a feasible starting point.
-
When only boundary constraints are specified:
-
If the parameter
, 
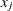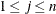, violates a two-sided boundary constraint (or an equality constraint) 
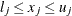, the parameter is given a new value inside the feasible interval, as follows:
![\[ x_ j = \left\{ \begin{array}{ll} l_ j, & \mr {if \: } u_ j \leq l_ j \\[0.1in] l_ j + \frac{1}{2}(u_ j - l_ j), & \mr {if \: } u_ j - l_ j < 4 \\[0.1in] l_ j + \frac{1}{10}(u_ j - l_ j), & \mr {if \: } u_ j - l_ j \geq 4 \end{array} \right. \]](images/ormplpug_nlp0367.png)
-
If the parameter
, 
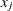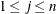, violates a one-sided boundary constraint 
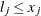or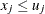 
, the parameter is given a new value near the violated boundary, as follows:
![\[ x_ j = \left\{ \begin{array}{ll} l_ j + \max (1, \frac{1}{10}l_ j), & \mr {if \: } x_ j < l_ j \\[0.1in] u_ j - \max (1, \frac{1}{10}u_ j), & \mr {if \: } x_ j > u_ j \end{array} \right. \]](images/ormplpug_nlp0371.png)
-
-
When general linear constraints are specified, the algorithm of Schittkowski and Stoer (1979) computes a feasible point, which may be quite far from a user-specified infeasible point.