Finite-Difference Approximations of Derivatives
The FD= and FDHESSIAN= options specify the use of finite-difference approximations of the derivatives. The FD= option specifies that all derivatives are approximated using function evaluations, and the FDHESSIAN= option specifies that second-order derivatives are approximated using gradient evaluations.
Computing derivatives by finite-difference approximations can be very time-consuming, especially for second-order derivatives based only on values of the objective function ( FD= option). If analytical derivatives are difficult to obtain (for example, if a function is computed by an iterative process), you might consider one of the optimization techniques that uses first-order derivatives only (TECH=QUANEW, TECH=DBLDOG, or TECH=CONGRA).
Forward-Difference Approximations
The forward-difference derivative approximations consume less computer time but are usually not as precise as those using central-difference formulas.
-
First-order derivatives:
 additional function calls are needed:
additional function calls are needed:
![\[ g_ i = \frac{\partial f}{\partial x_ i} = \frac{f(x + h_ ie_ i) - f(x)}{h_ i} \]](images/ormplpug_nlp0316.png)
-
Second-order derivatives based on function calls only (Dennis and Schnabel 1983, p. 80, 104): for dense Hessian,
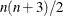 additional function calls are needed:
additional function calls are needed:
![\[ \frac{\partial ^2 f}{\partial x_ i \partial x_ j} = \frac{f(x+h_ ie_ i+h_ je_ j) - f(x+h_ ie_ i) - f(x+h_ je_ j) + f(x)}{h_ j} \]](images/ormplpug_nlp0318.png)
-
Second-order derivatives based on gradient calls (Dennis and Schnabel 1983, p. 103):
 additional gradient calls are needed:
additional gradient calls are needed:
![\[ \frac{\partial ^2 f}{\partial x_ i \partial x_ j} = \frac{g_ i(x + h_ je_ j) - g_ i(x)}{2h_ j} + \frac{g_ j(x + h_ ie_ i) - g_ j(x)}{2h_ i} \]](images/ormplpug_nlp0319.png)
Central-Difference Approximations
-
First-order derivatives:
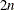 additional function calls are needed:
additional function calls are needed:
![\[ g_ i = \frac{\partial f}{\partial x_ i} = \frac{f(x + h_ ie_ i) - f(x - h_ ie_ i)}{2h_ i} \]](images/ormplpug_nlp0321.png)
-
Second-order derivatives based on function calls only (Abramowitz and Stegun 1972, p. 884): for dense Hessian,
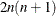 additional function calls are needed:
additional function calls are needed:
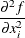
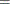
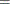
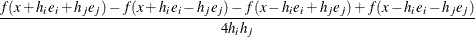
-
Second-order derivatives based on gradient:
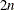 additional gradient calls are needed:
additional gradient calls are needed:
![\[ \frac{\partial ^2 f}{\partial x_ i \partial x_ j} = \frac{g_ i(x + h_ je_ j) - g_ i(x - h_ je_ j)}{4h_ j} + \frac{g_ j(x + h_ ie_ i) - g_ j(x - h_ ie_ i)}{4h_ i} \]](images/ormplpug_nlp0328.png)
The FDIGITS= and CDIGITS= options can be used for specifying the number of accurate digits in the evaluation of objective function and nonlinear constraints. These specifications are
helpful in determining an appropriate interval length ![]() to be used in the finite-difference formulas.
to be used in the finite-difference formulas.
The FDINT= option specifies whether the finite-difference intervals ![]() should be computed using an algorithm of Gill, Murray, Saunders, and Wright (1983) or based only on the information of the FDIGITS= and CDIGITS= options. For FDINT=OBJ, the interval
should be computed using an algorithm of Gill, Murray, Saunders, and Wright (1983) or based only on the information of the FDIGITS= and CDIGITS= options. For FDINT=OBJ, the interval ![]() is based on the behavior of the objective function; for FDINT=CON, the interval
is based on the behavior of the objective function; for FDINT=CON, the interval ![]() is based on the behavior of the nonlinear constraints functions; and for FDINT=ALL, the interval
is based on the behavior of the nonlinear constraints functions; and for FDINT=ALL, the interval ![]() is based on the behaviors of both the objective function and the nonlinear constraints functions. Note that the algorithm
of Gill, Murray, Saunders, and Wright (1983) to compute the finite-difference intervals
is based on the behaviors of both the objective function and the nonlinear constraints functions. Note that the algorithm
of Gill, Murray, Saunders, and Wright (1983) to compute the finite-difference intervals ![]() can be very expensive in the number of function calls. If the FDINT= option is specified, it is currently performed twice, the first time before the optimization process starts and the second
time after the optimization terminates.
can be very expensive in the number of function calls. If the FDINT= option is specified, it is currently performed twice, the first time before the optimization process starts and the second
time after the optimization terminates.
If FDINT= is not specified, the step lengths ![]() ,
, ![]() , are defined as follows:
, are defined as follows:
-
for the forward-difference approximation of first-order derivatives using function calls and second-order derivatives using gradient calls:
![$h_ j = \sqrt [2]{\eta _ j} (1 + |x_ j|)$](images/ormplpug_nlp0331.png) ,
,
-
for the forward-difference approximation of second-order derivatives that use only function calls and all central-difference formulas:
![$h_ j = \sqrt [3]{\eta _ j} (1 + |x_ j|)$](images/ormplpug_nlp0332.png) ,
,
where ![]() is defined using the FDIGITS= option:
is defined using the FDIGITS= option:
For FDINT=OBJ and FDINT=ALL, the FDIGITS= specification is used in computing the forward and central finite-difference intervals.
If the problem has nonlinear constraints and the FD= option is specified, the first-order formulas are used to compute finite-difference approximations of the Jacobian matrix
![]() . You can use the CDIGITS= option to specify the number of accurate digits in the constraint evaluations to define the step lengths
. You can use the CDIGITS= option to specify the number of accurate digits in the constraint evaluations to define the step lengths ![]() ,
, ![]() . For FDINT=CON and FDINT=ALL, the CDIGITS= specification is used in computing the forward and central finite-difference intervals.
. For FDINT=CON and FDINT=ALL, the CDIGITS= specification is used in computing the forward and central finite-difference intervals.
Note: If you are unable to specify analytic derivatives and the finite-difference approximations provided by PROC NLP are not good enough to solve your problem, you may program better finite-difference approximations using the GRADIENT, JACOBIAN, CRPJAC, or HESSIAN statement and the program statements.