Example 7.14 Generalized Networks: Distribution Problem
Consider a distribution problem (from Jensen and Bard 2003) with three supply plants (![]() –
– ![]() ) and five demand points (
) and five demand points (![]() –
– ![]() ). Further information about the problem is as follows:
). Further information about the problem is as follows:
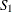
-
To be closed. Entire inventory must be shipped or sold to scrap. The scrap value is $5 per unit.
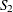
-
Maximum production of 300 units with manufacturing cost of $10 per unit.
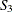
-
The production in regular time amounts to 200 units and must be shipped. An additional 100 units can be produced using overtime at $14 per unit.
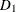
-
Fixed demand of 200 units must be met.
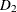
-
Contracted demand of 300 units. An additional 100 units can be sold at $20 per unit.
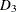
-
Minimum demand of 200 units. An additional 100 units can be sold at $20 per unit. Additional units can be procured from
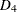 at $4 per unit. There is a 5% “shipping loss” on the arc connecting these two nodes.
at $4 per unit. There is a 5% “shipping loss” on the arc connecting these two nodes.
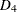
-
Fixed demand of 150 units must be met.
-
100 units left over from previous shipments. No firm demand, but up to 250 units can be sold at $25 per unit.
Additionally, there is a 5% “shipping loss” on each of the arcs between supply and demand nodes.
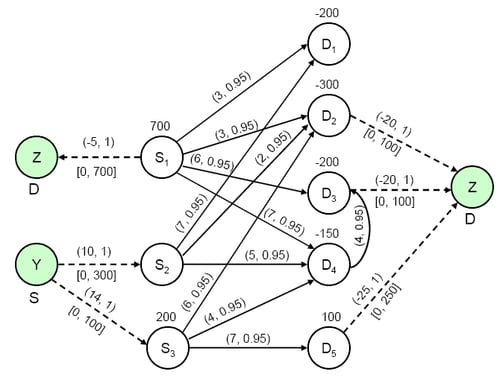
You can model this scenario as a generalized network. Since there are both fixed and varying supply and demand supdem values, you can transform this to a case where you need to address missing supply and demand simultaneously. As seen from
Output 7.14.1, we have added two artificial nodes, Y and Z, with missing S supply value and missing D demand value, respectively. The extra
production capability is depicted by arcs from node Y to the corresponding supply nodes, and the extra revenue generation
capability of the demand points (and scrap revenue for ![]() ) is depicted by arcs to node Z.
) is depicted by arcs to node Z.
Output 7.14.1: Distribution Problem
The following SAS data set has the complete information about the arc costs, multipliers, and node supdem values:
data dnodes; input _node_ $ _sd_ ; missing S D; datalines; S1 700 S2 0 S3 200 D1 -200 D2 -300 D3 -200 D4 -150 D5 100 Y S Z D ; data darcs; input _from_ $ _to_ $ _cost_ _capac_ _mult_; datalines; S1 D1 3 200 0.95 S1 D2 3 200 0.95 S1 D3 6 200 0.95 S1 D4 7 200 0.95 S2 D1 7 200 0.95 S2 D2 2 200 0.95 S2 D4 5 200 0.95 S3 D2 6 200 0.95 S3 D4 4 200 0.95 S3 D5 7 200 0.95 D4 D3 4 200 0.95 Y S2 10 300 . Y S3 14 100 . S1 Z -5 700 . D2 Z -20 100 . D3 Z -20 100 . D5 Z -25 250 . ;
You can solve this problem by using the following call to PROC NETFLOW:
title1 'The NETFLOW Procedure'; proc netflow nodedata = dnodes arcdata = darcs conout = dsol; run;
The optimal solution is displayed in Output 7.14.2.
Output 7.14.2: Distribution Problem: Optimal Solution
| The NETFLOW Procedure |
| Obs | _from_ | _to_ | _cost_ | _capac_ | _LO_ | _mult_ | _SUPPLY_ | _DEMAND_ | _FLOW_ | _FCOST_ |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | S1 | D1 | 3 | 200 | 0 | 0.95 | 700 | 200 | 200.000 | 600.00 |
| 2 | S2 | D1 | 7 | 200 | 0 | 0.95 | . | 200 | 10.526 | 73.68 |
| 3 | S1 | D2 | 3 | 200 | 0 | 0.95 | 700 | 300 | 200.000 | 600.00 |
| 4 | S2 | D2 | 2 | 200 | 0 | 0.95 | . | 300 | 200.000 | 400.00 |
| 5 | S3 | D2 | 6 | 200 | 0 | 0.95 | 200 | 300 | 21.053 | 126.32 |
| 6 | S1 | D3 | 6 | 200 | 0 | 0.95 | 700 | 200 | 200.000 | 1200.00 |
| 7 | D4 | D3 | 4 | 200 | 0 | 0.95 | . | 200 | 10.526 | 42.11 |
| 8 | S1 | D4 | 7 | 200 | 0 | 0.95 | 700 | 150 | 100.000 | 700.00 |
| 9 | S2 | D4 | 5 | 200 | 0 | 0.95 | . | 150 | 47.922 | 239.61 |
| 10 | S3 | D4 | 4 | 200 | 0 | 0.95 | 200 | 150 | 21.053 | 84.21 |
| 11 | S3 | D5 | 7 | 200 | 0 | 0.95 | 200 | . | 157.895 | 1105.26 |
| 12 | Y | S2 | 10 | 300 | 0 | 1.00 | S | . | 258.449 | 2584.49 |
| 13 | Y | S3 | 14 | 100 | 0 | 1.00 | S | . | 0.000 | 0.00 |
| 14 | S1 | Z | -5 | 700 | 0 | 1.00 | 700 | D | 0.000 | 0.00 |
| 15 | D2 | Z | -20 | 100 | 0 | 1.00 | . | D | 100.000 | -2000.00 |
| 16 | D3 | Z | -20 | 100 | 0 | 1.00 | . | D | 0.000 | 0.00 |
| 17 | D5 | Z | -25 | 250 | 0 | 1.00 | 100 | D | 250.000 | -6250.00 |
| -494.32 |