It is well known that in a pure network the sum of flows entering an arc is equal to the sum of flows leaving it. However, in a generalized network there may be a gain or a loss as flow traverses an arc. Each arc has a multiplier to represent these gains or losses.

To illustrate what is meant, consider the network shown in Figure 7.25.

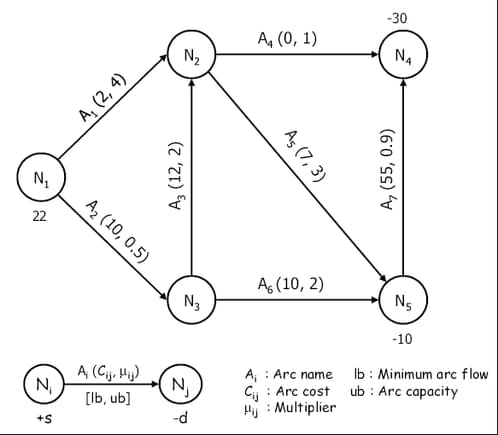
You can think of this as a network representing a supply node (), trans-shipment nodes (, ), and demand nodes (, ). As indicated by the legend, the number below a node represents its supdem value. Above each arc is its name, followed by the arc cost and arc multiplier in parentheses. The lower and upper bounds on flow allowed to enter an arc are represented in square brackets below it. When no bounds are specified (as in Figure 7.25), they are assumed to be [0, 99999999].

Now consider the node pair (, ). The information on arc says that it costs 2 per unit of flow to traverse it, and for each unit of flow entering the arc, four units get accumulated at node . The corresponding component in the objective function is two times the flow through arc leaving node , not two times the flow through arc arriving at node .

A commonly encountered example of a generalized network is in power generation: as electricity is transmitted over wires, there is some unavoidable loss along the way. This loss is represented by a multiplier less than 1.0.

Arc multipliers need not always be less than 1.0. For instance, in financial models, a flow through an arc could represent money in a bank account earning interest. In that case, the arc would have a multiplier greater than 1.0.

Generalized networks offer convenience when flow commodity changes. For a pure network, care must be taken to ensure the flow commodity is the same throughout the entire model. For example, in a model to determine how sugar should be grown, refined, packaged, and sold, the flow commodity might be kilograms of sugar, and all numerical parameters throughout the model (all supplies, arc costs, capacities, bounds, demands, etc.) must be in terms of kilograms of sugar. Some arcs might correspond to the movement of 5-kilogram bags of sugar. If a generalized network formulation is used, the arc that represents packaging could be given a multiplier of 0.2, so flow through arcs that convey flow corresponding to bags of sugar will have arc costs in terms of dollars per bag, and capacities, bounds, demands, etc. in terms of number of bags.

In the following sections we describe in detail how to provide data for arc multipliers, how to deal with excess supply or demand in pure and generalized networks, how to model maximum flow problems, and how to handle networks with missing supply and demand nodes, and ranges on supply and demand.