Network Models
A network consists of a collection of nodes joined by a collection of arcs. The arcs connect nodes and convey flow of one or more commodities that are supplied at supply nodes and demanded at demand nodes in the network. Each arc has a cost per unit of flow, a flow capacity, and a lower flow bound associated with it. An important concept in network modeling is conservation of flow.
Conservation of flow means that the total flow in arcs directed toward a node, plus the supply at the node, minus the demand at the node, equals the total flow in arcs directed away from the node.
A network and its associated data can be described in SAS data sets. PROC NETFLOW uses this description and finds the flow through each arc in the network that minimizes the total cost of flow, meets the demand at demand nodes using the supply at supply nodes so that the flow through each arc is on or between the arc’s lower flow bound and its capacity, and satisfies the conservation of flow.
One class of network models is the production-inventory-distribution problem. The diagram in Figure 7.1 illustrates this problem. The subscripts on the Production, Inventory, and Sales nodes indicate the time period. Notice that if you replicate sections of the model, the notion of time can be included.
Figure 7.1: Production-Inventory-Distribution Problem
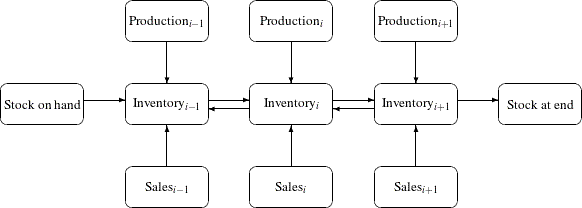
In this type of model, the nodes can represent a wide variety of facilities. Several examples are suppliers, spot markets, importers, farmers, manufacturers, factories, parts of a plant, production lines, waste disposal facilities, workstations, warehouses, coolstores, depots, wholesalers, export markets, ports, rail junctions, airports, road intersections, cities, regions, shops, customers, and consumers. The diversity of this selection demonstrates the richness of potential applications of this model.
Depending upon the interpretation of the nodes, the objectives of the modeling exercise can vary widely. Some common types of objectives are
-
to reduce collection or purchase costs of raw materials
-
to reduce inventory holding or backorder costs. Warehouses and other storage facilities sometimes have capacities, and there can be limits on the amount of goods that can be placed on backorder.
-
to decide where facilities should be located and what the capacity of these should be. Network models have been used to help decide where factories, hospitals, ambulance and fire stations, oil and water wells, and schools should be sited.
-
to determine the assignment of resources (machines, production capability, workforce) to tasks, schedules, classes, or files
-
to determine the optimal distribution of goods or services. This usually means minimizing transportation costs, and reducing time in transit or distances covered.
-
to find the shortest path from one location to another
-
to ensure that demands (for example, production requirements, market demands, contractual obligations) are met
-
to maximize profits from the sale of products or the charge for services
-
to maximize production by identifying bottlenecks
Some specific applications are
-
car distribution models. These help determine which models and numbers of cars should be manufactured in which factories and where to distribute cars from these factories to zones in the United States in order to meet customer demand at least cost.
-
models in the timber industry. These help determine when to plant and mill forests, schedule production of pulp, paper and wood products, and distribute products for sale or export.
-
military applications. The nodes can be theatres, bases, ammunition dumps, logistical suppliers, or radar installations. Some models are used to find the best ways to mobilize personnel and supplies and to evacuate the wounded in the least amount of time.
-
communications applications. The nodes can be telephone exchanges, transmission lines, satellite links, and consumers. In a model of an electrical grid, the nodes can be transformers, powerstations, watersheds, reservoirs, dams, and consumers. Of concern might be the effect of high loads or outages.