The LP Procedure

Example 5.13 A Scheduling Problem

Scheduling is an application area where techniques in model generation can be valuable. Problems involving scheduling are often solved with integer programming and are similar to assignment problems. In this example, you have eight one-hour time slots in each of five days. You have to assign four people to these time slots so that each slot is covered on every day. You allow the people to specify preference data for each slot on each day. In addition, there are constraints that must be satisfied:

Each person has some slots for which they are unavailable.
Each person must have either slot 4 or 5 off for lunch.
Each person can work only two time slots in a row.
Each person can work only a specified number of hours in the week.

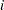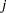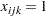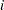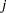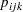To formulate this problem, let $\text{[math]}$ denote person, $\text{[math]}$ denote time slot, and $\text{[math]}$ denote day. 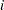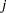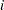Then, let $\text{[math]}$ if person $\text{[math]}$ is assigned to time slot $\text{[math]}$ on day $\text{[math]}$ , and 0 otherwise; let $\text{[math]}$ denote the preference of person $\text{[math]}$ for slot $\text{[math]}$ on day $\text{[math]}$ ; and let $\text{[math]}$ denote the number of hours in a week that person $\text{[math]}$ will work. Then, you get

$\text{[math]}$

To solve this problem, create a data set that has the hours and preference data for each individual, time slot, and day. A 10 represents the most desirable time slot, and a 1 represents the least desirable time slot. In addition, a 0 indicates that the time slot is not available.

data raw;
   input name $ hour slot mon tue wed thu fri;
   datalines;
marc  20   1    10 10 10 10 10
marc  20   2     9  9  9  9  9
marc  20   3     8  8  8  8  8
marc  20   4     1  1  1  1  1
marc  20   5     1  1  1  1  1
marc  20   6     1  1  1  1  1
marc  20   7     1  1  1  1  1
marc  20   8     1  1  1  1  1
mike  20   1    10  9  8  7  6
mike  20   2    10  9  8  7  6
mike  20   3    10  9  8  7  6
mike  20   4    10  3  3  3  3
mike  20   5     1  1  1  1  1
mike  20   6     1  2  3  4  5
mike  20   7     1  2  3  4  5
mike  20   8     1  2  3  4  5
bill  20   1    10 10 10 10 10
bill  20   2     9  9  9  9  9
bill  20   3     8  8  8  8  8
bill  20   4     0  0  0  0  0
bill  20   5     1  1  1  1  1
bill  20   6     1  1  1  1  1
bill  20   7     1  1  1  1  1
bill  20   8     1  1  1  1  1
bob   20   1    10  9  8  7  6
bob   20   2    10  9  8  7  6
bob   20   3    10  9  8  7  6
bob   20   4    10  3  3  3  3
bob   20   5     1  1  1  1  1
bob   20   6     1  2  3  4  5
bob   20   7     1  2  3  4  5
bob   20   8     1  2  3  4  5
;

These data are read by the following DATA step, and an integer program is built to solve the problem. The model is saved in the data set named MODEL. First, the objective function is built using the data saved in the RAW data set. Then, the constraints requiring a person to be working in each time slot are built. Next, the constraints allowing each person time for lunch are added. Then, the constraints restricting people to only two consecutive hours are added. Next, the constraints limiting the time that any one person works in a week are added. Finally, the constraints allowing a person to be assigned only to a time slot for which he is available are added. The code to build each of these constraints follows the formulation closely.

data model;
   array workweek{5} mon tue wed thu fri;
   array hours{4} hours1 hours2 hours3 hours4;
   retain hours1-hours4;

   set raw end=eof;

   length _row_ $ 8 _col_ $ 8 _type_ $ 8; 
   keep _type_ _col_ _row_ _coef_;

   if      name='marc' then i=1;
   else if name='mike' then i=2;
   else if name='bill' then i=3;
   else if name='bob'  then i=4;

   hours{i}=hour;

/* build the objective function */

do k=1 to 5;
   _col_='x'||put(i,1.)||put(slot,1.)||put(k,1.);

   _row_='object';
   _coef_=workweek{k} * 1000;
   output;
   _row_='upper';
   if workweek{k}^=0 then _coef_=1;
   output;
   _row_='integer';
   _coef_=1;
   output;
end;

/* build the rest of the model */

if eof then do;
   _coef_=.;
   _col_=' ';
   _type_='upper';
   _row_='upper';
   output;
   _type_='max';
   _row_='object';
   output;
   _type_='int';
   _row_='integer';
   output;

   /* every hour 1 person working */

   do j=1 to 8;
      do k=1 to 5;
         _row_='work'||put(j,1.)||put(k,1.);
         _type_='eq';
         _col_='_RHS_';
         _coef_=1;
         output;
         _coef_=1;
         _type_=' ';
         do i=1 to 4;
            _col_='x'||put(i,1.)||put(j,1.)||put(k,1.);
            output;
         end;
      end;
   end;

/* each person has a lunch */

do i=1 to 4;
   do k=1 to 5;
      _row_='lunch'||put(i,1.)||put(k,1.);
      _type_='le';
      _col_='_RHS_';
      _coef_=1;
      output;
      _coef_=1;
      _type_=' ';
      _col_='x'||put(i,1.)||'4'||put(k,1.);
      output;
      _col_='x'||put(i,1.)||'5'||put(k,1.);
      output;
   end;
end;

/* work at most 2 slots in a row */

do i=1 to 4;
   do k=1 to 5;
      do l=1 to 6;
      _row_='seq'||put(i,1.)||put(k,1.)||put(l,1.);
      _type_='le';
      _col_='_RHS_';
      _coef_=2;
       output;
      _coef_=1;
      _type_=' ';
         do j=0 to 2;
            _col_='x'||put(i,1.)||put(l+j,1.)||put(k,1.);
            output;
         end;
      end;
   end;
end;

/* work at most n hours in a week */

do i=1 to 4;
   _row_='capacit'||put(i,1.);
   _type_='le';
   _col_='_RHS_';
   _coef_=hours{i};
   output;
   _coef_=1;
   _type_=' ';
   do j=1 to 8;
      do k=1 to 5;
         _col_='x'||put(i,1.)||put(j,1.)||put(k,1.);
         output;
      end;
   end;
end;
end;
run;

The model saved in the data set named MODEL is in the sparse format. The constraint that requires one person to work in time slot 1 on day 2 is named WORK12; it is $\text{[math]}$ .

The following model is saved in the MODEL data set (which has 1387 observations).

   _TYPE_      _COL_    _ROW_       _COEF_

    eq        _RHS_    work12         1
              x112     work12         1
              x212     work12         1
              x312     work12         1
              x412     work12         1

The model is solved using the LP procedure. The option PRIMALOUT=SOLUTION causes PROC LP to save the primal solution in the data set named SOLUTION.

/* solve the linear program */

proc lp sparsedata noprint primalout=solution
   time=1000 maxit1=1000 maxit2=1000;
run;

The following DATA step takes the solution data set SOLUTION and generates a report data set named REPORT. It translates the variable names $\text{[math]}$ so that a more meaningful report can be written. Then, the PROC TABULATE procedure is used to display a schedule showing how the eight time slots are covered for the week.

/* report the solution */
title 'Reported Solution';

data report;
   set solution;
   keep name slot mon tue wed thu fri;
   if substr(_var_,1,1)='x' then do;
     if _value_>0 then do;
        n=substr(_var_,2,1);
        slot=substr(_var_,3,1);
        d=substr(_var_,4,1);
        if      n='1' then name='marc';
        else if n='2' then name='mike';
        else if n='3' then name='bill';
        else               name='bob';
        if      d='1' then mon=1;
        else if d='2' then tue=1;
        else if d='3' then wed=1;
        else if d='4' then thu=1;
        else               fri=1;
        output;
     end;
  end;
run;

proc format;
   value xfmt 1='  xxx   ';
run;

proc tabulate data=report;
   class name slot;
   var mon--fri;
   table (slot * name), (mon tue wed thu fri)*sum=' '*f=xfmt.
          /misstext=' ';
run;

Output 5.13.1 from PROC TABULATE summarizes the schedule. Notice that the constraint requiring that a person be assigned to each possible time slot on each day is satisfied.

Output 5.13.1 A Scheduling Problem

Reported Solution

		mon	tue	wed	thu	fri
slot	name	xxx	xxx	xxx	xxx	xxx
1	bill	xxx	xxx	xxx	xxx	xxx
2	bob	xxx
2	marc		xxx	xxx	xxx	xxx
3	marc			xxx	xxx	xxx
3	mike	xxx	xxx
4	mike	xxx	xxx	xxx	xxx	xxx
5	bob	xxx	xxx	xxx	xxx	xxx
6	bob		xxx			xxx
	marc	xxx
	mike			xxx	xxx
7	bill	xxx
	bob			xxx	xxx
	mike		xxx			xxx
8	bill	xxx
8	mike		xxx	xxx	xxx	xxx

Recall that PROC LP puts a character string in the macro variable _ORLP_ that describes the characteristics of the solution on termination. This string can be parsed using macro functions and the information obtained can be used in report writing. The variable can be written to the log with the command

%put &_orlp_;

which produces Figure 5.1.

Figure 5.1 _ORLP_ Macro Variable


 STATUS=SUCCESSFUL PHASE=3 OBJECTIVE=211000 P_FEAS=YES D_FEAS=YES 
         INT_ITER=0 INT_FEAS=1 ACTIVE=0 INT_BEST=211000 PHASE1_ITER=34 
         PHASE2_ITER=51 PHASE3_ITER=0

From this you learn, for example, that at termination the solution is integer optimal and has an objective value of 211000.