| Getting Started: LP Problems |
Data for an LP problem resembles the data for side constraints and nonarc variables supplied to PROC INTPOINT when solving an NPSC problem. It is also very similar to the data required by the LP procedure.
To solve LP problems using PROC INTPOINT, you save a representation of the LP variables and the constraints in one or two SAS data sets. These data sets are then passed to PROC INTPOINT for solution. There are various forms that a problem’s data can take. You can use any one or a combination of several of these forms.
The ARCDATA= data set contains information about the LP variables of the problem. Although this data set is called ARCDATA, it contains data for no arcs. Instead, all data in this data set are related to LP variables. This data set has no SAS variables containing values that are node names.
The ARCDATA= data set can be used to specify information about LP variables, including objective function coefficients, lower and upper value bounds, and names. These data are the elements of the vectors 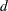 ,
,  , and
, and  in problem ( LP). Data for an LP variable can be given in more than one observation.
in problem ( LP). Data for an LP variable can be given in more than one observation.
The CONDATA= data set describes the constraints and their right-hand sides. These data are elements of the matrix 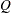 and the vector
and the vector  .
.
Constraint types are also specified in the CONDATA= data set. You can include in this data set LP variable data such as upper bound values, lower value bounds, and objective function coefficients. It is possible to give all information about some or all LP variables in the CONDATA= data set.
Because PROC INTPOINT evolved from PROC NETFLOW, another procedure in SAS/OR software that was originally designed to solve models with networks, the ARCDATA= data set is always expected. If the ARCDATA= data set is not specified, by default the last data set created before PROC INTPOINT is invoked is assumed to be the ARCDATA= data set. However, these characteristics of PROC INTPOINT are not helpful when an LP problem is being solved and all data are provided in a single data set specified by the CONDATA= data set, and that data set is not the last data set created before PROC INTPOINT starts. In this case, you must specify that the ARCDATA= data set and the CONDATA= data set are both equal to the input data set. PROC INTPOINT then knows that an LP problem is to be solved and that the data reside in one data set.
An LP variable is identified in this data set by its name. If you specify an LP variable’s name in the ARCDATA= data set, then this name is used to associate data in the CONDATA= data set with that LP variable.
If you use the dense constraint input format (described in the section CONDATA= Data Set), these LP variable names are names of SAS variables in the VAR list of the CONDATA= data set.
If you use the sparse constraint input format (described in the section CONDATA= Data Set), these LP variable names are values of the SAS variables in the COLUMN list of the CONDATA= data set.
PROC INTPOINT reads the data from the ARCDATA= data set (if there is one) and the CONDATA= data set. Error checking is performed, and the LP is preprocessed. Preprocessing is optional but highly recommended. The preprocessor analyzes the model and tries to determine before optimization whether LP variables can be "fixed" to their optimal values. Knowing that, the model can be modified and these LP variables dropped out. Some constraints may be found to be redundant. Sometimes, preprocessing succeeds in reducing the size of the problem, thereby making the subsequent optimization easier and faster.
The optimal solution is then found for the resulting LP. If the problem was preprocessed, the model is now post-processed, where fixed LP variables are reintroduced. The solution can be saved in the CONOUT= data set.
Introductory LP Example
Consider the linear programming problem in the section An Introductory Example. The SAS data set in that section is created the same way here:
title 'Linear Programming Example';
title3 'Setting Up Condata = dcon1 For PROC INTPOINT';
data dcon1;
input _id_ $17.
a_light a_heavy brega naphthal naphthai
heatingo jet_1 jet_2
_type_ $ _rhs_;
datalines;
profit -175 -165 -205 0 0 0 300 300 max .
naphtha_l_conv .035 .030 .045 -1 0 0 0 0 eq 0
naphtha_i_conv .100 .075 .135 0 -1 0 0 0 eq 0
heating_o_conv .390 .300 .430 0 0 -1 0 0 eq 0
recipe_1 0 0 0 0 .3 .7 -1 0 eq 0
recipe_2 0 0 0 .2 0 .8 0 -1 eq 0
available 110 165 80 . . . . . upperbd .
;
To solve this problem, use
proc intpoint bytes=1000000 condata=dcon1 conout=solutn1; run;
Note how it is possible to use an input SAS data set of PROC LP and, without requiring any changes to be made to the data set, to use that as an input data set for PROC INTPOINT.
The following messages that appear on the SAS log summarize the model as read by PROC INTPOINT and note the progress toward a solution
| NOTE: Number of variables= 8 . |
| NOTE: Number of <= constraints= 0 . |
| NOTE: Number of == constraints= 5 . |
| NOTE: Number of >= constraints= 0 . |
| NOTE: Number of constraint coefficients= 18 . |
| NOTE: After preprocessing, number of <= constraints= 0. |
| NOTE: After preprocessing, number of == constraints= 0. |
| NOTE: After preprocessing, number of >= constraints= 0. |
| NOTE: The preprocessor eliminated 5 constraints from the problem. |
| NOTE: The preprocessor eliminated 18 constraint coefficients from the problem. |
| NOTE: After preprocessing, number of variables= 0. |
| NOTE: The preprocessor eliminated 8 variables from the problem. |
| NOTE: The optimum has been determined by the Preprocessor. |
| NOTE: Objective= 1544. |
| NOTE: The data set WORK.SOLUTN1 has 8 observations and 6 variables. |
| NOTE: There were 7 observations read from the data set WORK.DCON1. |
Notice that the preprocessor succeeded in fixing all LP variables to their optimal values, eliminating the need to do any actual optimization.
Unlike PROC LP, which displays the solution and other information as output, PROC INTPOINT saves the optimum in the output SAS data set you specify. For this example, the solution is saved in the SOLUTION data set. It can be displayed with PROC PRINT as
title3 'LP Optimum'; proc print data=solutn1; var _name_ _objfn_ _upperbd _lowerbd _value_ _fcost_; sum _fcost_; run;
Notice that in the CONOUT=SOLUTION (Figure 4.9) the optimal value through each variable in the LP is given in the variable named _VALUE_, and that the cost of value for each variable is given in the variable _FCOST_.
| LP Optimum |
| Obs | _NAME_ | _OBJFN_ | _UPPERBD | _LOWERBD | _VALUE_ | _FCOST_ |
|---|---|---|---|---|---|---|
| 1 | a_heavy | -165 | 165 | 0 | 0.00 | 0 |
| 2 | a_light | -175 | 110 | 0 | 110.00 | -19250 |
| 3 | brega | -205 | 80 | 0 | 80.00 | -16400 |
| 4 | heatingo | 0 | 99999999 | 0 | 77.30 | 0 |
| 5 | jet_1 | 300 | 99999999 | 0 | 60.65 | 18195 |
| 6 | jet_2 | 300 | 99999999 | 0 | 63.33 | 18999 |
| 7 | naphthai | 0 | 99999999 | 0 | 21.80 | 0 |
| 8 | naphthal | 0 | 99999999 | 0 | 7.45 | 0 |
| 1544 |
The same model can be specified in the sparse format as in the following scon2 data set. This format enables you to omit the zero coefficients.
title3 'Setting Up Condata = scon2 For PROC INTPOINT'; data scon2; format _type_ $8. _col_ $8. _row_ $16.; input _type_ $ _col_ $ _row_ $ _coef_; datalines; max . profit . eq . napha_l_conv . eq . napha_i_conv . eq . heating_oil_conv . eq . recipe_1 . eq . recipe_2 . upperbd . available . . a_light profit -175 . a_light napha_l_conv .035 . a_light napha_i_conv .100 . a_light heating_oil_conv .390 . a_light available 110 . a_heavy profit -165 . a_heavy napha_l_conv .030 . a_heavy napha_i_conv .075 . a_heavy heating_oil_conv .300 . a_heavy available 165 . brega profit -205 . brega napha_l_conv .045 . brega napha_i_conv .135 . brega heating_oil_conv .430 . brega available 80 . naphthal napha_l_conv -1 . naphthal recipe_2 .2 . naphthai napha_i_conv -1 . naphthai recipe_1 .3 . heatingo heating_oil_conv -1 . heatingo recipe_1 .7 . heatingo recipe_2 .8 . jet_1 profit 300 . jet_1 recipe_1 -1 . jet_2 profit 300 . jet_2 recipe_2 -1 ;
To find the minimum cost solution, invoke PROC INTPOINT (note the SPARSECONDATA option which must be specified) as follows:
proc intpoint bytes=1000000 sparsecondata condata=scon2 conout=solutn2; run;
A data set that can be used as the ARCDATA= data set can be initialized as follows:
data vars3; input _name_ $ profit available; datalines; a_heavy -165 165 a_light -175 110 brega -205 80 heatingo 0 . jet_1 300 . jet_2 300 . naphthai 0 . naphthal 0 . ;
The following CONDATA= data set is the original dense format CONDATA= dcon1 data set after the LP variable’s nonconstraint information has been removed. (You could have left some or all of that information in CONDATA as PROC INTPOINT "merges" data, but doing that and checking for consistency takes time.)
data dcon3;
input _id_ $17.
a_light a_heavy brega naphthal naphthai
heatingo jet_1 jet_2
_type_ $ _rhs_;
datalines;
naphtha_l_conv .035 .030 .045 -1 0 0 0 0 eq 0
naphtha_i_conv .100 .075 .135 0 -1 0 0 0 eq 0
heating_o_conv .390 .300 .430 0 0 -1 0 0 eq 0
recipe_1 0 0 0 0 .3 .7 -1 0 eq 0
recipe_2 0 0 0 .2 0 .8 0 -1 eq 0
;
Note: You must now specify the MAXIMIZE option; otherwise, PROC INTPOINT will optimize to the minimum (which, incidentally, has a total objective = -3539.25). You must indicate that the SAS variable profit in the ARCDATA=vars3 data set has values that are objective function coefficients, by specifying the OBJFN statement. The UPPERBD must be specified as the SAS variable available that has as values upper bounds:
proc intpoint
maximize /* ***** necessary ***** */
bytes=1000000
arcdata=vars3
condata=dcon3
conout=solutn3;
objfn profit;
upperbd available;
run;
The ARCDATA=vars3 data set can become more concise by noting that the model variables heatingo, naphthai, and naphthal have zero objective function coefficients (the default) and default upper bounds, so those observations need not be present:
data vars4; input _name_ $ profit available; datalines; a_heavy -165 165 a_light -175 110 brega -205 80 jet_1 300 . jet_2 300 . ;
The CONDATA=dcon3 data set can become more concise by noting that all the constraints have the same type (eq) and zero (the default) rhs values. This model is a good candidate for using the DEFCONTYPE= option.
The DEFCONTYPE= option can be useful not only when all constraints have the same type as is the case here, but also when most constraints have the same type and you want to change the default type from  to
to 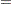 or
or  . The essential constraint type data in the CONDATA= data set is that which overrides the DEFCONTYPE= type you specified.
. The essential constraint type data in the CONDATA= data set is that which overrides the DEFCONTYPE= type you specified.
data dcon4;
input _id_ $17.
a_light a_heavy brega naphthal naphthai
heatingo jet_1 jet_2;
datalines;
naphtha_l_conv .035 .030 .045 -1 0 0 0 0
naphtha_i_conv .100 .075 .135 0 -1 0 0 0
heating_o_conv .390 .300 .430 0 0 -1 0 0
recipe_1 0 0 0 0 .3 .7 -1 0
recipe_2 0 0 0 .2 0 .8 0 -1
;
proc intpoint
maximize defcontype=eq
bytes=1000000
arcdata=vars3
condata=dcon3
conout=solutn3;
objfn profit;
upperbd available;
run;
Here are several different ways of using the ARCDATA= data set and a sparse format CONDATA= data set for this LP. The following CONDATA= data set is the result of removing the profit and available data from the original sparse format CONDATA=scon2 data set.
data scon5; format _type_ $8. _col_ $8. _row_ $16. ; input _type_ $ _col_ $ _row_ $ _coef_; datalines; eq . napha_l_conv . eq . napha_i_conv . eq . heating_oil_conv . eq . recipe_1 . eq . recipe_2 . . a_light napha_l_conv .035 . a_light napha_i_conv .100 . a_light heating_oil_conv .390 . a_heavy napha_l_conv .030 . a_heavy napha_i_conv .075 . a_heavy heating_oil_conv .300 . brega napha_l_conv .045 . brega napha_i_conv .135 . brega heating_oil_conv .430 . naphthal napha_l_conv -1 . naphthal recipe_2 .2 . naphthai napha_i_conv -1 . naphthai recipe_1 .3 . heatingo heating_oil_conv -1 . heatingo recipe_1 .7 . heatingo recipe_2 .8 . jet_1 recipe_1 -1 . jet_2 recipe_2 -1 ;
proc intpoint
maximize
bytes=1000000
sparsecondata
arcdata=vars3 /* or arcdata=vars4 */
condata=scon5
conout=solutn5;
objfn profit;
upperbd available;
run;
The CONDATA=scon5 data set can become more concise by noting that all the constraints have the same type (eq) and zero (the default) rhs values. Use the DEFCONTYPE= option again. Once the first five observations of the CONDATA=scon5 data set are removed, the _type_ variable has values that are missing in all of the remaining observations. Therefore, this variable can be removed.
data scon6; input _col_ $ _row_&$16. _coef_; datalines; a_light napha_l_conv .035 a_light napha_i_conv .100 a_light heating_oil_conv .390 a_heavy napha_l_conv .030 a_heavy napha_i_conv .075 a_heavy heating_oil_conv .300 brega napha_l_conv .045 brega napha_i_conv .135 brega heating_oil_conv .430 naphthal napha_l_conv -1 naphthal recipe_2 .2 naphthai napha_i_conv -1 naphthai recipe_1 .3 heatingo heating_oil_conv -1 heatingo recipe_1 .7 heatingo recipe_2 .8 jet_1 recipe_1 -1 jet_2 recipe_2 -1 ;
proc intpoint
maximize
bytes=1000000
defcontype=eq
sparsecondata
arcdata=vars4
condata=scon6
conout=solutn6;
objfn profit;
upperbd available;
run;