Logic-Based Puzzles
Previous Page|Next Page

The CLP Procedure

Example 3.1 Logic-Based Puzzles

Sudoku
Pi Day Sudoku
Magic Square

There are many logic-based puzzles that can be formulated as CSPs. Several such instances are shown in this example.

Sudoku

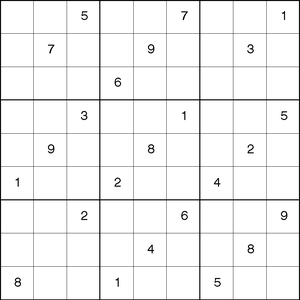
Sudoku is a logic-based, combinatorial number-placement puzzle played on a partially filled 9×9 grid. The objective is to fill the grid with the digits 1 to 9, so that each column, each row, and each of the nine 3×3 blocks contain only one of each digit. Output 3.1.1 shows an example of a Sudoku grid.

Output 3.1.1: An Example of an Unsolved Sudoku Grid

An Example of an Unsolved Sudoku Grid


This example illustrates the use of the ALLDIFFERENT constraint to solve the preceding Sudoku problem.

The data set indata contains the partially filled values for the grid and is used to create the set of macro variables $C_{ij}$ $(i=1 \ldots 9, j=1 \ldots 9)$, where $C_{ij}$ is the value of cell $(i,j)$ in the grid when specified, and missing otherwise. 

data indata;
   input C1-C9;
   datalines;
. . 5 . . 7 . . 1
. 7 . . 9 . . 3 .
. . . 6 . . . . .
. . 3 . . 1 . . 5
. 9 . . 8 . . 2 .
1 . . 2 . . 4 . .
. . 2 . . 6 . . 9
. . . . 4 . . 8 .
8 . . 1 . . 5 . .
;
run;     

%macro store_initial_values;
   /* store initial values into macro variable C_i_j */
   data _null_;
      set indata;
      array C{9};
      do j = 1 to 9;
         i = _N_;
         call symput(compress('C_'||put(i,best.)||'_'||put(j,best.)), 
            put(C[j],best.));
      end;
   run;
%mend store_initial_values; 

%store_initial_values;

Let the variable $X_{ij}$ $(i=1 \ldots 9, j=1 \ldots 9)$ represent the value of cell $(i,j)$ in the grid. The domain of each of these variables is $[1,9]$. Three sets of all-different constraints are used to set the required rules for each row, each column, and each of the 3×3 blocks. The constraint ALLDIFF($X_{i1}-X_{i9}$) forces all values in row $i$ to be different, the constraint ALLDIFF($X_{1j}-X_{9j}$) forces all values in column $j$ to be different, and the constraint ALLDIFF($X_{ij}$) $((i=1,2,3; j=1,2,3), (i=1,2,3; j=4,5,6), \ldots ,(i=7,8,9; j=7,8,9))$ forces all values in each block to be different.

The following statements solve the Sudoku puzzle: 

%macro solve;
   proc clp out=outdata;

      /* Declare variables    */
      /* Nine row constraints */
      %do i = 1 %to 9;
         var (X_&i._1-X_&i._9) = [1,9];
         alldiff(X_&i._1-X_&i._9);
      %end;

      /* Nine column constraints */
      %do j = 1 %to 9;
         alldiff(
         %do i = 1 %to 9;
            X_&i._&j
         %end;
         );
      %end;

      /* Nine 3x3 block constraints */
      %do s = 0 %to 2;
         %do t = 0 %to 2;
            alldiff(
            %do i = 3*&s + 1 %to 3*&s + 3;
               %do j = 3*&t + 1 %to 3*&t + 3;
                  X_&i._&j
               %end;
            %end;
            );
         %end;
      %end;

      /* Initialize variables to cell values   */
      /* X_i_j = C_i_j if C_i_j is non-missing */
      %do i = 1 %to 9;
         %do j = 1 %to 9;
            %if &&C_&i._&j ne . %then %do;
               lincon X_&i._&j = &&C_&i._&j;
            %end;
         %end;
      %end;

   run;
   %put &_ORCLP_;
%mend solve;
   
%solve

Output 3.1.2 shows the solution.

Output 3.1.2: Solution of the Sudoku Grid

Solution of the Sudoku Grid


The basic structure of the classical Sudoku problem can easily be extended to formulate more complex puzzles. One such example is the Pi Day Sudoku puzzle.

Pi Day Sudoku

Pi Day is a celebration of the number $\pi $ that occurs every March 14. In honor of Pi Day, Brainfreeze Puzzles (Riley and Taalman, 2008) celebrates this day with a special 12×12 grid Sudoku puzzle. The 2008 Pi Day Sudoku puzzle is shown in Output 3.1.3.

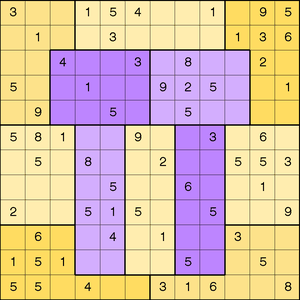
Output 3.1.3: Pi Day Sudoku 2008

Pi Day Sudoku 2008


The rules of this puzzle are a little different from the standard Sudoku. First, the blocks in this puzzle are jigsaw regions rather than 3×3 blocks. Each jigsaw region consists of $12$ contiguous cells. Second, the first $12$ digits of $\pi $ are used instead of the digits 1–9. Each row, column, and jigsaw region contains the first $12$ digits of $\pi $ ($3 1 4 1 5 9 2 6 5 3 5 8$) in some order. In particular, there are two $1$s, two $3$s, three $5$s, no $7$s, and one $2$, $4$, $6$, $8$, and $9$.

The data set raw contains the partially filled values for the grid and, similar to the Sudoku problem, is used to create the set of macro variables $C_{ij}$ $(i=1, \ldots ,12, j=1, \ldots ,12)$ where $C_{ij}$ is the value of cell $(i,j)$ in the grid when specified, and missing otherwise. 

data raw;
   input C1-C12;
   datalines;
3  .  .  1  5  4  .  .  1  .  9  5
.  1  .  .  3  .  .  .  .  1  3  6
.  .  4  .  .  3  .  8  .  .  2  .
5  .  .  1  .  .  9  2  5  .  .  1
.  9  .  .  5  .  .  5  .  .  .  .
5  8  1  .  .  9  .  .  3  .  6  .
.  5  .  8  .  .  2  .  .  5  5  3
.  .  .  .  5  .  .  6  .  .  1  .
2  .  .  5  1  5  .  .  5  .  .  9
.  6  .  .  4  .  1  .  .  3  .  .
1  5  1  .  .  .  .  5  .  .  5  .
5  5  .  4  .  .  3  1  6  .  .  8
;
run;

%macro cdata;
   /* store each pre-filled value into macro variable C_i_j */
   data _null_;
      set raw;
      array C{12};
      do j = 1 to 12;
         i = _N_;
         call symput(compress('C_'||put(i,best.)||'_'||put(j,best.)), 
            put(C[j],best.));
      end;
   run; 
%mend cdata;
%cdata;

As in the Sudoku problem, let the variable $X_{ij}$ represent the value of the cell that corresponds to row $i$ and column $j$. The domain of each of these variables is $[1, 9]$.

For each row, column, and jigsaw region, a GCC statement is specified to enforce the condition that it contain exactly the first twelve digits of $\pi $.

In particular, the variables in row $r$, $r = 1,\ldots ,12$ are $X_{r1},\ldots ,X_{r12}$. The SAS macro %CONS_ROW(R) enforces the GCC constraint that row $r$ contain exactly two $1$s, two $3$s, three $5$s, no $7$s, and one of each of the other values: 

%macro cons_row(r);
   /* Row r must contain two 1's, two 3's, three 5's, no 7's, */
   /* and one for each of other values from 1 to 9.           */
   gcc(X_&r._1-X_&r._12) =
      ( (1, 2, 2) (3, 2, 2) (5, 3, 3) (7, 0, 0) DL=1 DU=1 );
%mend cons_row;

The variables in column $c$ are $X_{1c},\dots ,X_{12c}$. The SAS macro %CONS_COL(C) enforces a similar GCC constraint for each column $c$. 

%macro cons_col(c);
   /* Column c must contain two 1's, two 3's, three 5's,    */
   /* no 7's, and one for each of other values from 1 to 9. */
   gcc( %do r = 1 %to 12;
      X_&r._&c.
      %end;
      ) = ((1, 2, 2) (3, 2, 2) (5, 3, 3) (7, 0, 0) DL=1 DU=1);
%mend cons_col;

Generalizing this concept further, the SAS macro %CONS_REGION(VARS) enforces the GCC constraint for the jigsaw region that is defined by the macro variable VARS. 

%macro cons_region(vars);
   /* Jigsaw region that contains &vars must contain two 1's, */
   /* two 3's, three 5's, no 7's, and one for each of other   */
   /* values from 1 to 9.                                     */
   gcc(&vars.) = ((1, 2, 2) (3, 2, 2) (5, 3, 3) (7, 0, 0) DL=1 DU=1);
%mend cons_region;

The following SAS statements incorporate the preceding macros to define the GCC constraints in order to find all solutions of the Pi Day Sudoku 2008 puzzle: 

%macro pds(solns=allsolns,varsel=MINR,maxt=900);

   proc clp out=pdsout &solns
            varselect=&varsel /* Variable selection strategy */
            maxtime=&maxt;    /* Time limit                  */

      /* Variable X_i_j represents the grid of ith row and jth column. */
      var (
         %do i = 1 %to 12;
            X_&i._1 - X_&i._12
         %end;
         ) = [1,9];
           
      /* X_i_j = C_i_j if C_i_j is non-missing */
      %do i = 1 %to 12;
         %do j = 1 %to 12;
            %if &&C_&i._&j ne . %then %do;
               lincon X_&i._&j = &&C_&i._&j;
            %end;
         %end;
      %end;
   
      /* 12 Row constraints: */
      %do r = 1 %to 12;
         %cons_row(&r);
      %end;

      /* 12 Column constraints: */
      %do c = 1 %to 12;
         %cons_col(&c);
      %end;

      /* 12 Jigsaw region constraints: */
      /* Each jigsaw region is defined by the macro variable &vars. */
         
      /* Region 1: */
      %let vars = X_1_1 - X_1_3 X_2_1 - X_2_3
                  X_3_1 X_3_2 X_4_1 X_4_2 X_5_1 X_5_2;
      %cons_region(&vars.);

      /* Region 2: */
      %let vars = X_1_4 - X_1_9 X_2_4 - X_2_9;
      %cons_region(&vars.);

      /* Region 3: */
      %let vars = X_1_10 - X_1_12 X_2_10 - X_2_12
                  X_3_11 X_3_12 X_4_11 X_4_12 X_5_11 X_5_12;
      %cons_region(&vars.);

      /* Region 4: */
      %let vars = X_3_3 - X_3_6 X_4_3 - X_4_6 X_5_3 - X_5_6;
      %cons_region(&vars.);

      /* Region 5: */
      %let vars = X_3_7 - X_3_10 X_4_7 - X_4_10 X_5_7 - X_5_10;
      %cons_region(&vars.);

      /* Region 6: */
      %let vars = X_6_1 - X_6_3 X_7_1 - X_7_3
                  X_8_1 - X_8_3 X_9_1 - X_9_3;
      %cons_region(&vars.);

      /* Region 7: */
      %let vars = X_6_4 X_6_5 X_7_4 X_7_5 X_8_4 X_8_5
                  X_9_4 X_9_5 X_10_4 X_10_5 X_11_4 X_11_5;
      %cons_region(&vars.);

      /* Region 8: */
      %let vars = X_6_6 X_6_7 X_7_6 X_7_7 X_8_6 X_8_7 
                  X_9_6 X_9_7 X_10_6 X_10_7 X_11_6 X_11_7;
      %cons_region(&vars.);

      /* Region 9: */
      %let vars = X_6_8 X_6_9 X_7_8 X_7_9 X_8_8 X_8_9 
                  X_9_8 X_9_9 X_10_8 X_10_9 X_11_8 X_11_9;
      %cons_region(&vars.);

      /* Region 10: */
      %let vars = X_6_10 - X_6_12 X_7_10 - X_7_12
                  X_8_10 - X_8_12 X_9_10 - X_9_12;
      %cons_region(&vars.);

      /* Region 11: */
      %let vars = X_10_1 - X_10_3 X_11_1 - X_11_3 X_12_1 - X_12_6;
      %cons_region(&vars.);

      /* Region 12: */
      %let vars = X_10_10 - X_10_12 X_11_10 - X_11_12 X_12_7 - X_12_12;
      %cons_region(&vars.);
   run;
   %put &_ORCLP_;

%mend pds;

%pds;

The only solution of the 2008 Pi Day Sudoku puzzle is shown in Output 3.1.4.

Output 3.1.4: Solution to Pi Day Sudoku 2008

Pi Day Sudoku 2008

Obs C1 C2 C3 C4 C5 C6 C7 C8 C9 C10 C11 C12
1 3 2 5 1 5 4 6 3 1 8 9 5
2 4 1 5 2 3 8 5 9 5 1 3 6
3 6 1 4 5 9 3 5 8 3 1 2 5
4 5 3 3 1 8 5 9 2 5 6 4 1
5 8 9 2 6 5 1 1 5 4 3 3 5
6 5 8 1 5 2 9 4 3 3 5 6 1
7 1 5 3 8 1 6 2 4 9 5 5 3
8 9 4 5 3 5 1 5 6 8 2 1 3
9 2 3 6 5 1 5 3 1 5 4 8 9
10 3 6 8 9 4 5 1 5 1 3 5 2
11 1 5 1 3 6 3 8 5 2 9 5 4
12 5 5 9 4 3 2 3 1 6 5 1 8


The corresponding completed grid is shown in Output 3.1.5.

Output 3.1.5: Solution to Pi Day Sudoku 2008

Solution to Pi Day Sudoku 2008


Magic Square

A magic square is an arrangement of the distinct positive integers from 1 to $n^2$ in an $n\times n$ matrix such that the sum of the numbers of any row, any column, or any main diagonal is the same number, known as the magic constant. The magic constant of a normal magic square depends only on $n$ and has the value $n(n^2+1)/2.$

This example illustrates the use of the EVALVARSEL= option to solve a magic square of size seven. When the EVALVARSEL option is specified without a keyword list, the CLP procedure evaluates each of the available variable selection strategies for the amount of time specified by the MAXTIME= option. In this example, MINRMAXC is the only variable selection strategy that finds a solution within three seconds. The macro variable _ORCLPEVS_ contains the results for each selection strategy. 

%macro magic(n);
   %put n = &n;
   /* magic constant */
   %let sum = %eval((&n*(&n*&n+1))/2);
   proc clp out=magic&n evalvarsel maxtime=3;
      /* X_i_j = entry (i,j) */
      %do i = 1 %to &n;
         var (X_&i._1-X_&i._&n) = [1,%eval(&n*&n)];
      %end;
      /* row sums */
      %do i = 1 %to &n;
         lincon 0
         %do j = 1 %to &n;
             + X_&i._&j
         %end;
         = ∑
      %end;
      /* column sums */
      %do j = 1 %to &n;
         lincon 0
         %do i = 1 %to &n;
            + X_&i._&j
         %end;
         = ∑
      %end;
      /* diagonal: upper left to lower right */
      lincon 0
      %do i = 1 %to &n;
         + X_&i._&i
      %end;
      = ∑
      /* diagonal: upper right to lower left */
      lincon 0
      %do i = 1 %to &n;
         + X_%eval(&n+1-&i)_&i
      %end;
      = ∑
      /* symmetry-breaking */
      lincon X_1_1  + 1 <= X_&n._1;
      lincon X_1_1  + 1 <= X_&n._&n;
      lincon X_1_&n + 1 <= X_&n._1;

      alldiff();
   run;      
   %put &_ORCLP_;
   %put &_ORCLPEVS_;
%mend magic;

%magic(7);

The solution is displayed in Output 3.1.6.

Output 3.1.6: Solution of the Magic Square

Solution of the Magic Square


Previous Page|Next Page|Top of Page
Copyright © SAS Institute Inc. All Rights Reserved.