FNONCT Function

Returns the value of the noncentrality parameter of an F distribution.

Category:

Mathematical

Syntax

FNONCT(x,ndf,ddf,prob)

Required Arguments

x

is a numeric random variable.

Range

x ≥ 0

ndf

is a numeric numerator degree of freedom parameter.

Range

ndf > 0

ddf

is a numeric denominator degree of freedom parameter.

Range

ddf > 0

prob

is a probability.

Range

0 < prob < 1

Details

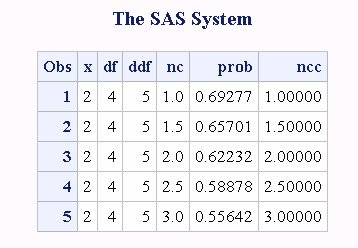
The FNONCT function returns the nonnegative noncentrality parameter from a noncentral F distribution whose parameters are x, ndf, ddf, and nc. If prob is greater than the probability from the central F distribution whose parameters are x, ndf, and ddf, a root to this problem does not exist. In this case a missing value is returned. A Newton-type algorithm is used to find a nonnegative root nc of the equation

\begin{matrix} P_{f} (x | n d f, d d f, n c) - p r o b = 0 \end{matrix}

The following relationship applies to the preceding equation:

\begin{matrix} P_{f} (x | n d f, d d f, n c) = ε^{\frac{- n c}{2}} Σ_{j = 0}^{\infty} \frac{{(\frac{n c}{2})}^{j}}{j!} I_{\frac{(n d f) x}{d d f + (n d f) x}} (\frac{d d f}{2} + j, \frac{d d f}{2}) \end{matrix}

In the equation, I (. . .) is the probability from the beta distribution that is given by the following equation:

\begin{matrix} I_{x} (a, b) = \frac{}{\frac{Γ (a) Γ (b)}{Γ (a + b)}} \int_{0}^{x} t^{a - 1} {(1 - t)}^{b - 1} d t \end{matrix}

If the algorithm fails to converge to a fixed point, a missing value is returned.

Example

data work;
   x=2;
   df=4;
   ddf=5;
   do nc=1 to 3 by .5;
      prob=probf(x,df,ddf,nc);
      ncc=fnonct(x,df,ddf,prob);
      output;
   end;
run;
proc print;
run;

FNONCT Example Output