PROBMC Function
Returns a probability or a quantile from various distributions for multiple comparisons of means.
| Category: | Probability |
Syntax
Required Arguments
distribution
is a character constant, variable, or expression that identifies the distribution. The following are valid distributions:
q
is the quantile from the distribution.
| Restriction | Either q or prob can be specified, but not both. |
prob
is the left probability from the distribution.
| Restriction | Either prob or q can be specified, but not both. |
Optional Argument
parameters
is an optional set of nparms parameters that must be specified to handle the case of unequal sample sizes. The meaning of parameters depends on the value of distribution. If parameters is not specified, equal sample sizes are assumed, which is usually the case for a null hypothesis.
Details
Overview
Computing the Analysis of Means
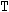 vector, with
degrees of freedom, and an associated correlation
matrix
. This equation can be written as
vector, with
degrees of freedom, and an associated correlation
matrix
. This equation can be written as
Computing the Partitioned Range
Williams' Test
Examples
Example 1: Computing Probabilities by Using PROBMC
Example 2: Computing the Analysis of Means
Example 3: Comparing Means
data duncan;
array tr{7}$;
array mu{7};
n=7;
do i=1 to n;
input tr{i} $1. mu{i};
end;
input df s alpha;
prob= 1-alpha;
/* compute the interval */
x = probmc("RANGE", ., prob, df, 7);
w = x * s / sqrt(6);
/* compare the means */
do i = 1 to n;
do j = i + 1 to n;
dmean = abs(mu{i} - mu{j});
if dmean >= w then do;
put tr{i} tr{j} dmean;
end;
end;
end;
datalines;
A 49.6
B 71.2
C 67.6
D 61.5
E 71.3
F 58.1
G 61.0
30 8.924 .05
;
run;Example 4: Computing the Partitioned Range
Example 5: Computing Confidence Intervals
data a;
array drug{3}$;
array count{3};
array mu{3};
array lambda{2};
array delta{2};
array left{2};
array right{2};
/* input the table */
do i = 1 to 3;
input drug{i} count{i} mu{i};
end;
/* input the alpha level, */
/* the degrees of freedom, */
/* and the mean square error */
input alpha df s;
/* from the sample size, */
/* compute the lambdas */
do i = 1 to 2;
lambda{i} = sqrt(count{i}/
(count{i} + count{3}));
end;
/* run the one-sided Dunnett's test */
test="dunnett1";
x = probmc(test, ., 1 - alpha, df,
2, of lambda1-lambda2);
do i = 1 to 2;
delta{i} = x * s *
sqrt(1/count{i} + 1/count{3});
left{i} = mu{i} - mu{3} - delta{i};
end;
put test $10. x left{1} left{2};
/* run the two-sided Dunnett's test */
test="dunnett2";
x = probmc(test, ., 1 - alpha, df,
2, of lambda1-lambda2);
do i=1 to 2;
delta{i} = x * s *
sqrt(1/count{i} + 1/count{3});
left{i} = mu{i} - mu{3} - delta{i};
right{i} = mu{i} - mu{3} + delta{i};
end;
put test $10. left{1} right{1};
put test $10. left{2} right{2};
datalines;
A 4 8.90
B 5 10.88
C 6 8.25
0.05 12 1.175
;
run;