Wavelet Analysis
Some Brief Mathematical Preliminaries
The discrete wavelet transform decomposes a function as a sum of basis functions called wavelets. These basis functions have
the property that they can be obtained by dilating and translating two basic types of wavelets known as the scaling function, or father wavelet  , and The mother wavelet
, and The mother wavelet 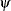 . These translations and dilations are defined as follows:
. These translations and dilations are defined as follows:
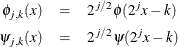
The index j defines the dilation or level while the index k defines the translate. Loosely speaking, sums of the 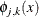 capture low frequencies and sums of the
capture low frequencies and sums of the 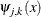 represent high frequencies in the data. More precisely, for any suitable function
represent high frequencies in the data. More precisely, for any suitable function 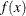 and for any
and for any 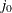 ,
,
![\[ f(x)= \sum _ k c^{j_0}_ k \phi _{j_0,k}(x) + \sum _{j \geq j_0} \sum _ k d^ j_ k \psi _{j,k}(x) \]](images/imlug_waveletanalysis0008.png)
where the 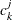 and
and 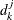 are known as the scaling coefficients and the detail coefficients, respectively. For orthonormal wavelet families these coefficients
can be computed by
are known as the scaling coefficients and the detail coefficients, respectively. For orthonormal wavelet families these coefficients
can be computed by
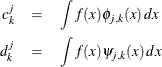
The key to obtaining fast numerical algorithms for computing the detail and scaling coefficients for a given function 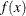 is that there are simple recurrence relationships that enable you to compute the coefficients at level
is that there are simple recurrence relationships that enable you to compute the coefficients at level 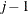 from the values of the scaling coefficients at level j. These formulas are
from the values of the scaling coefficients at level j. These formulas are
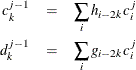
The coefficients 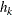 and
and 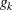 that appear in these formulas are called filter coefficients. The
that appear in these formulas are called filter coefficients. The 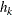 are determined by the father wavelet and they form a low-pass filter;
are determined by the father wavelet and they form a low-pass filter; 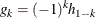 and form a high-pass filter. The preceding sums are formally over the entire (infinite) range of integers. However, for wavelets
that are zero except on a finite interval, only finitely many of the filter coefficients are nonzero, and so in this case
the sums in the recurrence relationships for the detail and scaling coefficients are finite.
and form a high-pass filter. The preceding sums are formally over the entire (infinite) range of integers. However, for wavelets
that are zero except on a finite interval, only finitely many of the filter coefficients are nonzero, and so in this case
the sums in the recurrence relationships for the detail and scaling coefficients are finite.
Conversely, if you know the detail and scaling coefficients at level 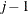 , then you can obtain the scaling coefficients at level j by using the relationship
, then you can obtain the scaling coefficients at level j by using the relationship
![\[ c^ j_ k = \sum _ i h_{k-2i} c^{j-1}_ i + \sum _ i g_{k-2i}d^{j-1}_ i \]](images/imlug_waveletanalysis0017.png)
Suppose that you have data values
![\[ y_ k = f(x_ k), \qquad k=0,1,2,\cdots ,N-1 \]](images/imlug_waveletanalysis0018.png)
at 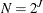 equally spaced points
equally spaced points 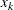 . It turns out that the values
. It turns out that the values 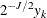 are good approximations of the scaling coefficients
are good approximations of the scaling coefficients 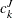 . Then, by using the recurrence formula, you can find
. Then, by using the recurrence formula, you can find 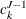 and
and 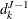 ,
, 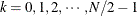 . The discrete wavelet transform of the
. The discrete wavelet transform of the 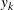 at level
at level 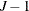 consists of the
consists of the 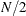 scaling and
scaling and 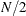 detail coefficients at level
detail coefficients at level 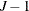 . A technical point that arises is that in applying the recurrence relationships to finite data, a few values of the
. A technical point that arises is that in applying the recurrence relationships to finite data, a few values of the 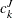 for
for 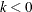 or
or 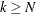 might be needed. One way to cope with this difficulty is to extend the sequence
might be needed. One way to cope with this difficulty is to extend the sequence 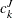 to the left and right by using some specified boundary treatment.
to the left and right by using some specified boundary treatment.
Continuing by replacing the scaling coefficients at any level j by the scaling and detail coefficients at level j – 1 yields a sequence of N coefficients
![\[ \{ c^0_0,d^0_0,d^1_0,d^1_1,d^2_0,d^2_1,d^2_2,d^2_3,d^3_1,\ldots ,d^3_7,\ldots ,d^{J-1}_0,\ldots ,d^{J-1}_{N/2-1}\} \]](images/imlug_waveletanalysis0031.png)
This sequence is the finite discrete wavelet transform of the input data 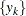 . At any level
. At any level 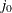 the finite dimensional approximation of the function
the finite dimensional approximation of the function 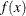 is
is
![\[ f(x)\approx \sum _ k c^{j_0}_ k \phi _{j_0,k}(x) + \sum _{j=j_0}^{J-1} \sum _ k d^ j_ k \psi _{j,k}(x) \]](images/imlug_waveletanalysis0033.png)
