Time Series Analysis and Examples

Example 14.3 Diffuse Kalman Filtering

The nonstationary SSM is simulated to analyze the diffuse Kalman filter call KALDFF. The transition equation is generated by using the formula

$\left[ \begin{array}{c} z_{1t} \\ z_{2t} \end{array} \right] = \left[ \begin{array}{cc} 1.5 & -0.5 \\ 1.0 & 0.0 \end{array} \right] \left[ \begin{array}{c} z_{1t-1} \\ z_{2t-1} \end{array} \right] + \left[ \begin{array}{c} \eta _{1t} \\ 0 \end{array} \right]$

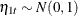where $\eta _{1t} \sim N(0,1)$ . The transition equation is nonstationary because the transition matrix 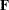$\bF$ has one unit root. The following program simulates a time series:

title 'Diffuse Kalman Filtering';
proc iml;
T = 20;
y = j(T,1);
burnIn = 10;
z_1 = 0; z_2 = 0;
do i = 1-burnIn to T;
   z = 1.5*z_1 - 0.5*z_2 + rannor(1234567);
   z_2 = z_1;  z_1 = z;
   x = z + 0.8*rannor(1234567);
   if ( i > 0 ) then
      y[i] = x;
end;

The KALDFF and KALCVF calls produce one-step prediction, and the following program shows that two predictions coincide after the fifth observation. See Output 14.3.1.

h = { 1 0 };
f = { 1.5 -.5, 1 0 };
rt = .64;
vt = diag({1 0});
ny = nrow(h);
nz = ncol(h);
nb = nz;
nd = nz;
a  = j(nz,1,0);
b  = j(ny,1,0);
int = j(ny+nz,nb,0);
coef = f // h;
var = ( vt || j(nz,ny,0) ) //
      ( j(ny,nz,0) || rt );
intd = j(nz+nb,1,0);
coefd = i(nz) // j(nb,nd,0);
at = j(t*nz,nd+1,0);
mt = j(t*nz,nz,0);
qt = j(t*(nd+1),nd+1,0);
n0 = -1;
call kaldff(kaldff_p,dvpred,initial,s2,y,0,int,
            coef,var,intd,coefd,n0,at,mt,qt);
call kalcvf(kalcvf_p,vpred,filt,vfilt,y,0,a,f,b,h,var);
print kalcvf_p kaldff_p;

Output 14.3.1: Diffuse Kalman Filtering

Diffuse Kalman Filtering

kalcvf_p		kaldff_p
0	0	0	0
1.441911	0.961274	1.1214871	0.9612746
-0.882128	-0.267663	-0.882138	-0.267667
-0.723156	-0.527704	-0.723158	-0.527706
1.2964969	0.871659	1.2964968	0.8716585
-0.035692	0.1379633	-0.035692	0.1379633
-2.698135	-1.967344	-2.698135	-1.967344
-5.010039	-4.158022	-5.010039	-4.158022
-9.048134	-7.719107	-9.048134	-7.719107
-8.993153	-8.508513	-8.993153	-8.508513
-11.16619	-10.44119	-11.16619	-10.44119
-10.42932	-10.34166	-10.42932	-10.34166
-8.331091	-8.822777	-8.331091	-8.822777
-9.578258	-9.450848	-9.578258	-9.450848
-6.526855	-7.241927	-6.526855	-7.241927
-5.218651	-5.813854	-5.218651	-5.813854
-5.01855	-5.291777	-5.01855	-5.291777
-6.5699	-6.284522	-6.5699	-6.284522
-4.613301	-4.995434	-4.613301	-4.995434
-5.057926	-5.09007	-5.057926	-5.09007

The likelihood function for the diffuse Kalman filter under the finite initial covariance matrix 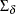$\Sigma _\delta$ is written as

$\lambda (\mb{y}) = -\frac{1}{2}[\mb{y}^\# \log (\hat{\sigma }^2) + \sum _{t=1}^ T \log (|\bD _ t|)]$

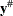where $\mb{y}^{\# }$ is the dimension of the matrix 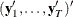$(\mb{y}^{\prime }_1, \ldots , \mb{y}^{\prime }_ T)^{\prime }$ . The likelihood function for the diffuse Kalman filter under the diffuse initial covariance matrix 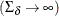$(\Sigma _\delta \rightarrow \infty )$ is computed as 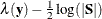$\lambda (\mb{y}) - \frac{1}{2}\log (|\bS |)$ , where the 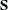$\bS$ matrix is the upper 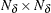$N_\delta \times N_\delta$ matrix of 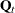$\bQ _ t$ . Output 14.3.2 displays the log likelihood and the diffuse log likelihood, as computed by the following statements:

d = 0;
do i = 1 to t;
   dt = h*mt[(i-1)*nz+1:i*nz,]*h` + rt;
   d = d + log(det(dt));
end;
s = qt[(t-1)*(nd+1)+1:t*(nd+1)-1,1:nd];
log_l = -(t*log(s2) + d)/2;
dff_logl = log_l - log(det(s))/2;
print log_l[L='Log L']  dff_logl[L='Diffuse Log L'];
quit;

Output 14.3.2: Diffuse Likelihood Function

Log L	Diffuse Log L
-11.42547	-9.457596