Time Series Analysis and Examples
Example 14.2 Kalman Filtering: SSM Estimation with the EM Algorithm
The following example estimates the normal SSM of the mink-muskrat data (Harvey 1989) by using the EM algorithm. The mink-muskrat data are log-counts that have been detrended.
title 'SSM Estimation Using EM Algorithm'; data MinkMuskrat; input muskrat mink @@; datalines; 0.10609 0.16794 -0.16852 0.06242 -0.23700 -0.13344 -0.18022 -0.50616 0.18094 -0.37943 0.65983 -0.40132 0.65235 0.08789 0.21594 0.23877 -0.11515 0.40043 -0.00067 0.37758 -0.00387 0.55735 -0.25202 0.34444 -0.65011 -0.02749 -0.53646 -0.41519 -0.08462 0.02591 -0.05640 -0.11348 0.26630 0.20544 0.03641 0.16331 -0.26030 -0.01498 -0.03995 0.09657 0.33612 0.31096 -0.11672 0.30681 -0.69775 -0.69351 -0.07569 -0.56212 0.36149 -0.36799 0.42341 -0.24725 0.26721 0.04478 -0.00363 0.21637 0.08333 0.30188 -0.22480 0.29493 -0.13728 0.35463 -0.12698 0.05490 -0.18770 -0.52573 0.34741 -0.49541 0.54947 -0.26250 0.57423 -0.21936 0.57493 -0.12012 0.28188 0.63556 -0.58438 0.27067 -0.50236 0.10386 -0.60766 0.36748 -1.04784 -0.33493 -0.68857 -0.46525 -0.11450 -0.63648 0.22005 -0.26335 0.36533 0.07017 -0.00151 -0.04977 0.03740 -0.02411 0.22438 0.30790 -0.16196 0.41050 -0.12862 0.34929 0.08448 -0.14995 0.17945 -0.03320 0.37502 0.02953 0.95727 0.24090 0.86188 0.41096 0.39464 0.24157 0.53794 0.29385 0.13054 0.39336 -0.39138 -0.00323 -1.23825 -0.56953 -0.66286 -0.72363 ;
Because this EM algorithm uses filtering and smoothing, you can use the KALCVF and KALCVS calls to analyze the data. Consider the bivariate SSM,
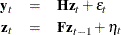
where 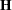 is a
is a 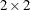 identity matrix, the observation noise has a time-invariant covariance matrix
identity matrix, the observation noise has a time-invariant covariance matrix 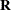 , and the covariance matrix of the transition equation is also assumed to be time-invariant. The initial state
, and the covariance matrix of the transition equation is also assumed to be time-invariant. The initial state 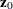 has mean
has mean 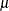 and covariance
and covariance 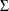 . For estimation, the
. For estimation, the 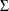 matrix is fixed as
matrix is fixed as
![\[ \left[ \begin{array}{cc} 0.1 & 0.0 \\ 0.0 & 0.1 \end{array} \right] \]](images/imlug_timeseriesexpls0055.png)
whereas the mean vector 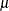 is updated by the smoothing procedure such that
is updated by the smoothing procedure such that 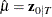 . Note that this estimation requires an extra smoothing step, because the usual smoothing procedure does not produce
. Note that this estimation requires an extra smoothing step, because the usual smoothing procedure does not produce 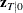 .
.
The EM algorithm maximizes the expected log-likelihood function, given the current parameter estimates. In practice, the log-likelihood function of the normal SSM is evaluated while the parameters are updated by using the M-step of the EM maximization,
![\begin{eqnarray*} \bF ^{i+1} & = & \bS _ t(1)[\bS _{t-1}(0)]^{-1} \\ \bV ^{i+1} & = & \frac{1}{T} \left( \bS _ t(0) - \bS _ t(1)[\bS _{t-1}(0)]^{-1} \bS ^{\prime }_ t(1) \right) \\ \bR ^{i+1} & = & \frac{1}{T} \sum _{t=1}^ T \left[ (\mb{y}_ t - \bH \mb{z}_{t|T}) (\mb{y}_ t - \bH \mb{z}_{t|T})^{\prime } + \bH \bP _{t|T} \bH ^{\prime } \right] \\ \mu ^{i+1} & = & \mb{z}_{0|T} \end{eqnarray*}](images/imlug_timeseriesexpls0058.png)
where the index i represents the current iteration number, and
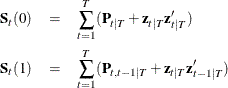
It is necessary to compute the value of 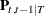 recursively such that
recursively such that
![\[ \bP _{t-1,t-2|T} = \bP _{t-1|t-1} \bP ^{*\prime }_{t-2} + \bP ^*_{t-1} (\bP _{t,t-1|T} - \bF \bP _{t-1|t-1}) \bP ^{*\prime }_{t-2} \]](images/imlug_timeseriesexpls0061.png)
where 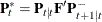 and the initial value
and the initial value 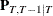 is derived by using the formula
is derived by using the formula
![\[ \bP _{T,T-1|T} = \left[ \bI - \bP _{t|t-1} \bH ^{\prime } (\bH \bP _{t|t-1} \bH ^{\prime } + \bR )^{-1} \bH \right] \bF \bP _{T-1|T-1} \]](images/imlug_timeseriesexpls0064.png)
Note that the initial value of the state vector is updated for each iteration,
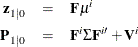
The objective function value is computed as 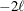 in the SAS/IML module LIK. The log-likelihood function is written as
in the SAS/IML module LIK. The log-likelihood function is written as
![\[ \ell = -\frac{1}{2} \sum _{t=1}^ T \log (|\bC _ t|) - \frac{1}{2} \sum _{t=1}^ T (\mb{y}_ t - \bH \mb{z}_{t|t-1}) \bC ^{-1}_ t (\mb{y}_ t - \bH \mb{z}_{t|t-1})^{\prime } \]](images/imlug_timeseriesexpls0067.png)
where 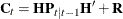 .
.
The EM algorithm is implemented by the following statements. The iteration history is shown in Output 14.2.1.
proc iml;
start lik(y,pred,vpred,h,rt);
n = nrow(y);
nz = ncol(h);
et = y - pred*h`;
sum1 = 0;
sum2 = 0;
do i = 1 to n;
vpred_i = vpred[(i-1)*nz+1:i*nz,];
et_i = et[i,];
ft = h*vpred_i*h` + rt;
sum1 = sum1 + log(det(ft));
sum2 = sum2 + et_i*inv(ft)*et_i`;
end;
return(sum1+sum2);
finish;
use MinkMuskrat;
read all into y var {muskrat mink};
close MinkMuskrat;
/*-- mean adjust series --*/
t = nrow(y); ny = ncol(y); nz = ny;
f = i(nz);
h = i(ny);
/*-- observation noise variance is diagonal --*/
rt = 1e-5#i(ny);
/*-- transition noise variance --*/
vt = .1#i(nz);
a = j(nz,1,0);
b = j(ny,1,0);
myu = j(nz,1,0);
sigma = .1#i(nz);
converge = 0;
logl0 = 0.0;
do iter = 1 to 100 while( converge = 0 );
/*--- construct big cov matrix --*/
var = ( vt || j(nz,ny,0) ) //
( j(ny,nz,0) || rt );
/*-- initial values are changed --*/
z0 = myu` * f`;
vz0 = f * sigma * f` + vt;
/*-- filtering to get one-step prediction and filtered value --*/
call kalcvf(pred,vpred,filt,vfilt,y,0,a,f,b,h,var,z0,vz0);
/*-- smoothing using one-step prediction values --*/
call kalcvs(sm,vsm,y,a,f,b,h,var,pred,vpred);
/*-- compute likelihood values --*/
logl = lik(y,pred,vpred,h,rt);
/*-- store old parameters and function values --*/
myu0 = myu;
f0 = f;
vt0 = vt;
rt0 = rt;
diflog = logl - logl0;
logl0 = logl;
itermat = itermat // ( iter || logl0 || shape(f0,1) || myu0` );
/*-- obtain P*(t) to get P_T_0 and Z_T_0 --*/
/*-- these values are not usually needed --*/
/*-- See Harvey (1989, p154) or Shumway (1988, p177) --*/
jt1 = sigma * f` * inv(vpred[1:nz,]);
p_t_0 = sigma + jt1*(vsm[1:nz,] - vpred[1:nz,])*jt1`;
z_t_0 = myu + jt1*(sm[1,]` - pred[1,]`);
p_t1_t = vpred[(t-1)*nz+1:t*nz,];
p_t1_t1 = vfilt[(t-2)*nz+1:(t-1)*nz,];
kt = p_t1_t*h`*inv(h*p_t1_t*h`+rt);
/*-- obtain P_T_TT1. See Shumway (1988, p180) --*/
p_t_ii1 = (i(nz)-kt*h)*f*p_t1_t1;
st0 = vsm[(t-1)*nz+1:t*nz,] + sm[t,]`*sm[t,];
st1 = p_t_ii1 + sm[t,]`*sm[t-1,];
st00 = p_t_0 + z_t_0 * z_t_0`;
cov = (y[t,]` - h*sm[t,]`) * (y[t,]` - h*sm[t,]`)` +
h*vsm[(t-1)*nz+1:t*nz,]*h`;
do i = t to 2 by -1;
p_i1_i1 = vfilt[(i-2)*nz+1:(i-1)*nz,];
p_i1_i = vpred[(i-1)*nz+1:i*nz,];
jt1 = p_i1_i1 * f` * inv(p_i1_i);
p_i1_i = vpred[(i-2)*nz+1:(i-1)*nz,];
if ( i > 2 ) then
p_i2_i2 = vfilt[(i-3)*nz+1:(i-2)*nz,];
else
p_i2_i2 = sigma;
jt2 = p_i2_i2 * f` * inv(p_i1_i);
p_t_i1i2 = p_i1_i1*jt2` + jt1*(p_t_ii1 - f*p_i1_i1)*jt2`;
p_t_ii1 = p_t_i1i2;
temp = vsm[(i-2)*nz+1:(i-1)*nz,];
sm1 = sm[i-1,]`;
st0 = st0 + ( temp + sm1 * sm1` );
if ( i > 2 ) then
st1 = st1 + ( p_t_ii1 + sm1 * sm[i-2,]);
else st1 = st1 + ( p_t_ii1 + sm1 * z_t_0`);
st00 = st00 + ( temp + sm1 * sm1` );
cov = cov + ( h * temp * h` +
(y[i-1,]` - h * sm1)*(y[i-1,]` - h * sm1)` );
end;
/*-- M-step: update the parameters --*/
myu = z_t_0;
f = st1 * inv(st00);
vt = (st0 - st1 * inv(st00) * st1`)/t;
rt = cov / t;
/*-- check convergence --*/
if ( max(abs((myu - myu0)/(myu0+1e-6))) < 1e-2 &
max(abs((f - f0)/(f0+1e-6))) < 1e-2 &
max(abs((vt - vt0)/(vt0+1e-6))) < 1e-2 &
max(abs((rt - rt0)/(rt0+1e-6))) < 1e-2 &
abs((diflog)/(logl0+1e-6)) < 1e-3 ) then
converge = 1;
end;
reset noname;
colnm = {'Iter' '-2*log L' 'F11' 'F12' 'F21' 'F22'
'MYU11' 'MYU22'};
print itermat[colname=colnm format=8.4];
Output 14.2.1: Iteration History
| SSM Estimation Using EM Algorithm |
| Iter | -2*log L | F11 | F12 | F21 | F22 | MYU11 | MYU22 |
|---|---|---|---|---|---|---|---|
| 1.0000 | -154.010 | 1.0000 | 0.0000 | 0.0000 | 1.0000 | 0.0000 | 0.0000 |
| 2.0000 | -237.962 | 0.7952 | -0.6473 | 0.3263 | 0.5143 | 0.0530 | 0.0840 |
| 3.0000 | -238.083 | 0.7967 | -0.6514 | 0.3259 | 0.5142 | 0.1372 | 0.0977 |
| 4.0000 | -238.126 | 0.7966 | -0.6517 | 0.3259 | 0.5139 | 0.1853 | 0.1159 |
| 5.0000 | -238.143 | 0.7964 | -0.6519 | 0.3257 | 0.5138 | 0.2143 | 0.1304 |
| 6.0000 | -238.151 | 0.7963 | -0.6520 | 0.3255 | 0.5136 | 0.2324 | 0.1405 |
| 7.0000 | -238.153 | 0.7962 | -0.6520 | 0.3254 | 0.5135 | 0.2438 | 0.1473 |
| 8.0000 | -238.155 | 0.7962 | -0.6521 | 0.3253 | 0.5135 | 0.2511 | 0.1518 |
| 9.0000 | -238.155 | 0.7962 | -0.6521 | 0.3253 | 0.5134 | 0.2558 | 0.1546 |
| 10.0000 | -238.155 | 0.7961 | -0.6521 | 0.3253 | 0.5134 | 0.2588 | 0.1565 |
The following statements compute the eigenvalues of 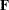 . As shown in Output 14.2.2, the eigenvalues of
. As shown in Output 14.2.2, the eigenvalues of 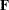 are within the unit circle, indicating that the SSM is stationary. However, the muskrat series is reported to be difference
stationary. The estimated parameters are almost identical to those of the VAR(1) estimates. See Harvey (1989).
are within the unit circle, indicating that the SSM is stationary. However, the muskrat series is reported to be difference
stationary. The estimated parameters are almost identical to those of the VAR(1) estimates. See Harvey (1989).
eval = eigval(f0);
colnm = {'Real' 'Imag' 'MOD'};
eval = eval || sqrt((eval#eval)[,+]);
print eval[colname=colnm];
Output 14.2.2: Eigenvalues of F Matrix
Finally, multistep forecasts of 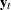 are computed by calling the KALCVF subroutine. The predicted values of the state vector
are computed by calling the KALCVF subroutine. The predicted values of the state vector 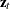 and their standard errors are shown in Output 14.2.3.
and their standard errors are shown in Output 14.2.3.
var = ( vt || j(nz,ny,0) ) //
( j(ny,nz,0) || rt );
/*-- initial values are changed --*/
z0 = myu` * f`;
vz0 = f * sigma * f` + vt;
free itermat;
/*-- multistep prediction --*/
call kalcvf(pred,vpred,filt,vfilt,y,15,a,f,b,h,var,z0,vz0);
do i = 1 to 15;
itermat = itermat // ( i || pred[t+i,] ||
sqrt(vecdiag(vpred[(t+i-1)*nz+1:(t+i)*nz,]))` );
end;
colnm = {'n-Step' 'Z1_T_n' 'Z2_T_n' 'SE_Z1' 'SE_Z2'};
print itermat[colname=colnm];
quit;
Output 14.2.3: Multistep Prediction
| n-Step | Z1_T_n | Z2_T_n | SE_Z1 | SE_Z2 |
|---|---|---|---|---|
| 1 | -0.055792 | -0.587049 | 0.2437666 | 0.237074 |
| 2 | 0.3384325 | -0.319505 | 0.3140478 | 0.290662 |
| 3 | 0.4778022 | -0.053949 | 0.3669731 | 0.3104052 |
| 4 | 0.4155731 | 0.1276996 | 0.4021048 | 0.3218256 |
| 5 | 0.2475671 | 0.2007098 | 0.419699 | 0.3319293 |
| 6 | 0.0661993 | 0.1835492 | 0.4268943 | 0.3396153 |
| 7 | -0.067001 | 0.1157541 | 0.430752 | 0.3438409 |
| 8 | -0.128831 | 0.0376316 | 0.4341532 | 0.3456312 |
| 9 | -0.127107 | -0.022581 | 0.4369411 | 0.3465325 |
| 10 | -0.086466 | -0.052931 | 0.4385978 | 0.3473038 |
| 11 | -0.034319 | -0.055293 | 0.4393282 | 0.3479612 |
| 12 | 0.0087379 | -0.039546 | 0.4396666 | 0.3483717 |
| 13 | 0.0327466 | -0.017459 | 0.439936 | 0.3485586 |
| 14 | 0.0374564 | 0.0016876 | 0.4401753 | 0.3486415 |
| 15 | 0.0287193 | 0.0130482 | 0.440335 | 0.3487034 |