Robust Regression Examples

If you do not specify a design matrix 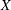for the last input argument, the regression problem reduces to the problem of estimating the location parameter. That is, the "intercept-only" regression model is equivalent to estimating the location parameter for the response variable. For ordinary least squares regression, an intercept-only regression model estimates the mean. For robust regression, it estimates a robust measure of location.

The following example is described in Rousseeuw and Leroy (1987); Barnett and Lewis (1994).

proc iml;
y = { 3, 4, 7, 8, 10, 949, 951 };

optn = j(9,1,.);
call lms(scLMS, coefLMS, wgtLMS, optn, y);
call lts(scLTS, coefLTS, wgtLTS, optn, y);

LMSOutliers = loc(wgtLMS[1,]=0);
LTSOutliers = loc(wgtLTS[1,]=0);
print LMSOutliers, LTSOutliers;

rLoc = {"Mean", "Median", "LMS Location", "LTS Location"};
Loc  = mean(y) // median(y) // coefLMS[1] // coefLTS[1];
print Loc[r=rLoc L="Location Estimates"];

rScale = {"StdDev", "MAD", "LMS Scale", "LTS Scale"};
Scale =    std(y) // mad(y) // scLMS[7] // scLTS[7];
print Scale[r=rScale L="Scale Estimates"];

Output 13.3.1 shows that the LMS and LTS subroutines both classify observations 6 and 7 as outliers.

Output 13.3.1 shows several estimates of the central location of the data. The classical mean (276) is highly influenced by the two large values. In contrast, the median of the data is 8, and the LMS and LTS estimates are both 5.5. Output 13.3.1 also shows estimates of the scale of the data. The classical standard deviation (460.4) is influenced by the two large values. In contrast, the MAD function computes the median absolute deviation to be 4. The LMS and LTS estimates are both 3.05. The scale estimate in the univariate problem is a resistant (high-breakdown) estimator for the dispersion of the data (Rousseeuw and Leroy 1987).