Nonlinear Optimization Examples

Example 15.8 Time-Optimal Heat Conduction

The following example illustrates a nontrivial application of the NLPQN algorithm that requires nonlinear constraints, which are specified by the nlc module. The example is listed as problem 91 in Hock and Schittkowski (1981). The problem describes a time-optimal heating process minimizing the simple objective function

\[ f(x) = \sum _{j=1}^ n x_ j^2 \]

subjected to a rather difficult inequality constraint:

\[ c(x) = 10^{-4} - h(x) \ge 0 \]

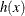where $h(x)$ is defined as

\begin{eqnarray*} h(x) & = & \int _0^1 \left( \sum _{i=1}^{30} \alpha _ i(s) \rho _ i(x) - k_0(s) \right)^2 ~ ds \\ \alpha _ i(s) & = & \mu _ i^2 A_ i \cos (\mu _ i s) \\ \rho _ i(x) & = & - \mu _ i^2 \Biggl [ \exp \left( -\mu _ i^2 \sum _{j=1}^ n x_ j^2 \right) - 2 \exp \left( -\mu _ i^2 \sum _{j=2}^ n x_ j^2 \right) + \cdots \\[0.1in]& & \qquad + (-1)^{n-1} 2 \exp \left( -\mu _ i^2 x_ n^2 \right) + (-1)^ n \Biggr ] \\[0.1in] k_0(s) & = & 0.5 (1 - s^2) \\ A_ i & = & \frac{2 \sin \mu _ i}{\mu _ i + \sin \mu _ i \cos \mu _ i}, \\ \mu & = & (\mu _1,\ldots ,\mu _{30})^{\prime } \mbox{ , where } \mu _ i \tan (\mu _ i) = 1 \end{eqnarray*}

The gradient of the objective function f, 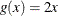$g(x) = 2x$, is easily supplied to the NLPQN subroutine. However, the analytical derivatives of the constraint are not used; instead, finite-difference derivatives are computed.

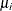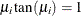In the following code, the vector MU represents the first 30 positive values $\mu _ i$ that satisfy $\mu _ i \tan (\mu _ i) = 1$: 

proc iml;
/* Vector mu[30] found by solving mu[j] * tan(mu[j]) = 1 */
mu = {
   8.6033358901938E-01 ,    3.4256184594817E+00 ,
   6.4372981791719E+00 ,    9.5293344053619E+00 ,
   1.2645287223856E+01 ,    1.5771284874815E+01 ,
   1.8902409956860E+01 ,    2.2036496727938E+01 ,
   2.5172446326646E+01 ,    2.8309642854452E+01 ,
   3.1447714637546E+01 ,    3.4586424215288E+01 ,
   3.7725612827776E+01 ,    4.0865170330488E+01 ,
   4.4005017920830E+01 ,    4.7145097736761E+01 ,
   5.0285366337773E+01 ,    5.3425790477394E+01 ,
   5.6566344279821E+01 ,    5.9707007305335E+01 ,
   6.2847763194454E+01 ,    6.5988598698490E+01 ,
   6.9129502973895E+01 ,    7.2270467060309E+01 ,
   7.5411483488848E+01 ,    7.8552545984243E+01 ,
   8.1693649235601E+01 ,    8.4834788718042E+01 ,
   8.7975960552493E+01 ,    9.1117161394464E+01  };

The vector 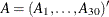$A=(A_1,\ldots ,A_{30})^{\prime }$ depends only on 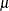$\mu $ and is computed only once, before the optimization starts, as follows: 

/* Vector a[nmu] depends only on mu and is computed once */
nmu  = nrow(mu);
a = j(1,nmu,0.);
do i = 1 to nmu;
   a[i] = 2*sin(mu[i]) / (mu[i] + sin(mu[i])*cos(mu[i]));
end;

The constraint is implemented with the QUAD subroutine, which performs numerical integration of scalar functions in one dimension. The subroutine calls the module fquad that supplies the integrand for 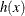$h(x)$. For details about the QUAD call, see the section QUAD Call. Here is the code: 

/* This is the integrand used in h(x) */
start fquad(s) global(mu,rho);
   z = (rho * cos(s*mu) - 0.5*(1. - s##2))##2;
   return(z);
finish;

/* Obtain nonlinear constraint h(x) */
start h(x) global(n,nmu,mu,a,rho);
   xx = x##2;
   do i= n-1 to 1 by -1;
      xx[i] = xx[i+1] + xx[i];
   end;
   rho = j(1,nmu,0.);
   do i=1 to nmu;
      mu2 = mu[i]##2;
      sum = 0; t1n = -1.;
      do j=2 to n;
         t1n = -t1n;
         sum = sum + t1n * exp(-mu2*xx[j]);
      end;
      sum = -2*sum + exp(-mu2*xx[1]) + t1n;
      rho[i] = -a[i] * sum;
   end;
   aint = do(0,1,.5);
   call quad(z,"fquad",aint) eps=1.e-10;
   v = sum(z);
   return(v);
finish;

The modules for the objective function, its gradient, and the constraint 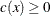$c(x) \ge 0$ are given in the following code: 

/* Define modules for NLPQN call: f, g, and c */
start F_HS88(x);
   f = x * x`;
   return(f);
finish F_HS88;

start G_HS88(x);
   g = 2 * x;
   return(g);
finish G_HS88;

start C_HS88(x);
   c = 1.e-4 - h(x);
   return(c);
finish C_HS88;

The number of constraints returned by the "nlc" module is defined by opt$[10]=1$. The ABSGTOL termination criterion (maximum absolute value of the gradient of the Lagrange function) is set by tc$[6]=1$E–4. Here is the code: 

title 'Hock & Schittkowski Problem #91 (1981) n=5, INSTEP=1';
opt  = j(1,10,.);
opt[2]=3;
opt[10]=1;
tc   = j(1,12,.);
tc[6]=1.e-4;
x0 = {.5 .5 .5 .5 .5};
n = ncol(x0);

call nlpqn(rc,rx,"F_HS88",x0,opt,,tc) grd="G_HS88" nlc="C_HS88";
quit;

Part of the iteration history and the parameter estimates are shown in Output 15.8.1.

Output 15.8.1: Iteration History and Parameter Estimates

Hock & Schittkowski Problem #91 (1981) n=5, INSTEP=1

Parameter Estimates 5
Nonlinear Constraints 1

Optimization Start
Objective Function 1.25 Maximum Constraint Violation 0.0952775105
Maximum Gradient of the Lagran Func 1.1433393264    

Iteration   Restarts Function
Calls 		Objective
Function 		Maximum
Constraint
Violation 		Predicted
Function
Reduction 		Step
Size 		Maximum
Gradient
Element
of the
Lagrange
Function
1   0 3 0.81165 0.0869 1.7562 0.100 1.325
2   0 4 0.18232 0.1175 0.6220 1.000 1.207
3 * 0 5 0.34576 0.0690 0.9318 1.000 0.640
4   0 6 0.77689 0.0132 0.3496 1.000 1.328
5   0 7 0.54995 0.0239 0.3403 1.000 1.334
6   0 9 0.55322 0.0212 0.4327 0.242 0.423
7   0 10 0.75884 0.00828 0.1545 1.000 0.630
8   0 12 0.76720 0.00681 0.3810 0.300 0.248
9   0 13 0.94843 0.00237 0.2186 1.000 1.857
10   0 15 0.95661 0.00207 0.3707 0.184 0.795
11   0 16 1.11201 0.000690 0.2575 1.000 0.591
12   0 18 1.14603 0.000494 0.2810 0.370 1.483
13   0 20 1.19821 0.000311 0.1991 0.491 2.014
14   0 22 1.22804 0.000219 0.2292 0.381 1.155
15   0 23 1.31506 0.000056 0.0697 1.000 1.578
16   0 25 1.31759 0.000051 0.0876 0.100 1.006
17   0 26 1.35547 7.337E-6 0.0133 1.000 0.912
18   0 27 1.36136 1.644E-6 0.00259 1.000 1.064
19   0 28 1.36221 4.263E-7 0.000902 1.000 0.0325
20   0 29 1.36266 9.79E-10 2.063E-6 1.000 0.00273
21   0 30 1.36266 5.73E-12 1.031E-6 1.000 0.00011
22   0 31 1.36266 0 2.044E-6 1.000 0.00001

Optimization Results
Iterations 22 Function Calls 32
Gradient Calls 24 Active Constraints 1
Objective Function 1.3626578338 Maximum Constraint Violation 0
Maximum Projected Gradient 3.2132973E-6 Value Lagrange Function 1.3626568149
Maximum Gradient of the Lagran Func 2.957267E-6 Slope of Search Direction -2.043849E-6

Hock & Schittkowski Problem #91 (1981) n=5, INSTEP=1

Optimization Results
Parameter Estimates
N Parameter Estimate Gradient
Objective
Function 		Gradient
Lagrange
Function
1 X1 0.860193 1.720386 0.000001798
2 X2 6.0264249E-8 0.000000121 0.000000341
3 X3 0.643607 1.287214 -0.000000306
4 X4 -0.456614 -0.913228 0.000002957
5 X5 -7.390521E-9 -1.478104E-8 -1.478104E-8 




            

            


            
Problems 88 to 92 of Hock and Schittkowski (1981) specify the same optimization problem for n = 2 to n = 6. You can solve any of these problems with the preceding code by submitting a vector of length n as the initial estimate, 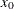$x_0$.