Nonlinear Optimization Examples
Example 15.7 A Two-Equation Maximum Likelihood Problem
The following example and notation are taken from Bard (1974). A two-equation model is used to fit U.S. production data for the years 1909–1949, where 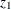 is capital input,
is capital input, 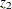 is labor input,
is labor input, 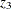 is real output,
is real output, 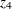 is time in years (with 1929 as the origin), and
is time in years (with 1929 as the origin), and 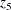 is the ratio of price of capital services to wage scale. The data can be entered by using the following statements:
is the ratio of price of capital services to wage scale. The data can be entered by using the following statements:
proc iml;
z={ 1.33135 0.64629 0.4026 -20 0.24447,
1.39235 0.66302 0.4084 -19 0.23454,
1.41640 0.65272 0.4223 -18 0.23206,
1.48773 0.67318 0.4389 -17 0.22291,
1.51015 0.67720 0.4605 -16 0.22487,
1.43385 0.65175 0.4445 -15 0.21879,
1.48188 0.65570 0.4387 -14 0.23203,
1.67115 0.71417 0.4999 -13 0.23828,
1.71327 0.77524 0.5264 -12 0.26571,
1.76412 0.79465 0.5793 -11 0.23410,
1.76869 0.71607 0.5492 -10 0.22181,
1.80776 0.70068 0.5052 -9 0.18157,
1.54947 0.60764 0.4679 -8 0.22931,
1.66933 0.67041 0.5283 -7 0.20595,
1.93377 0.74091 0.5994 -6 0.19472,
1.95460 0.71336 0.5964 -5 0.17981,
2.11198 0.75159 0.6554 -4 0.18010,
2.26266 0.78838 0.6851 -3 0.16933,
2.33228 0.79600 0.6933 -2 0.16279,
2.43980 0.80788 0.7061 -1 0.16906,
2.58714 0.84547 0.7567 0 0.16239,
2.54865 0.77232 0.6796 1 0.16103,
2.26042 0.67880 0.6136 2 0.14456,
1.91974 0.58529 0.5145 3 0.20079,
1.80000 0.58065 0.5046 4 0.18307,
1.86020 0.62007 0.5711 5 0.18352,
1.88201 0.65575 0.6184 6 0.18847,
1.97018 0.72433 0.7113 7 0.20415,
2.08232 0.76838 0.7461 8 0.18847,
1.94062 0.69806 0.6981 9 0.17800,
1.98646 0.74679 0.7722 10 0.19979,
2.07987 0.79083 0.8557 11 0.21115,
2.28232 0.88462 0.9925 12 0.23453,
2.52779 0.95750 1.0877 13 0.20937,
2.62747 1.00285 1.1834 14 0.19843,
2.61235 0.99329 1.2565 15 0.18898,
2.52320 0.94857 1.2293 16 0.17203,
2.44632 0.97853 1.1889 17 0.18140,
2.56478 1.02591 1.2249 18 0.19431,
2.64588 1.03760 1.2669 19 0.19492,
2.69105 0.99669 1.2708 20 0.17912 };
The two-equation model in five parameters 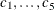 is
is
![\begin{eqnarray*} g_1 & = & c_110^{c_2z_4}[c_5z_1^{-c_4} + (1-c_5)z_2^{-c_4}]^{-c_3/c_4} - z_3 = 0 \\ g_2 & = & [\frac{c_5}{1-c_5}] \left( \frac{z_1}{z_2} \right)^{-1-c_4} -z_5 = 0 \end{eqnarray*}](images/imlug_nonlinearoptexpls0373.png)
where the variables 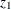 and
and 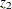 are considered dependent (endogenous) and the variables
are considered dependent (endogenous) and the variables 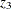 ,
, 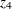 , and
, and 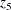 are considered independent (exogenous).
are considered independent (exogenous).
Differentiation of the two equations 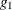 and
and 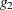 with respect to the endogenous variables
with respect to the endogenous variables 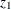 and
and 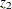 yields the Jacobian matrix
yields the Jacobian matrix 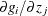 for
for 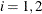 and
and 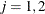 , where i corresponds to rows (equations) and j corresponds to endogenous variables (refer to Bard (1974)). You must consider parameter sets for which the elements of the Jacobian and the logarithm of the determinant cannot be
computed. In such cases, the function module must return a missing value.
, where i corresponds to rows (equations) and j corresponds to endogenous variables (refer to Bard (1974)). You must consider parameter sets for which the elements of the Jacobian and the logarithm of the determinant cannot be
computed. In such cases, the function module must return a missing value.
Assuming that the residuals of the two equations are normally distributed, the likelihood is then computed as in Bard (1974). The following code computes the logarithm of the likelihood function:
start fiml(pr) global(z);
c1 = pr[1]; c2 = pr[2]; c3 = pr[3]; c4 = pr[4]; c5 = pr[5];
/* 1. Compute Jacobian */
lndet = 0 ;
do t= 1 to 41;
j11 = (-c3/c4) * c1 * 10 ##(c2 * z[t,4]) * (-c4) * c5 *
z[t,1]##(-c4-1) * (c5 * z[t,1]##(-c4) + (1-c5) *
z[t,2]##(-c4))##(-c3/c4 -1);
j12 = (-c3/c4) * (-c4) * c1 * 10 ##(c2 * z[t,4]) * (1-c5) *
z[t,2]##(-c4-1) * (c5 * z[t,1]##(-c4) + (1-c5) *
z[t,2]##(-c4))##(-c3/c4 -1);
j21 = (-1-c4)*(c5/(1-c5))*z[t,1]##( -2-c4)/ (z[t,2]##(-1-c4));
j22 = (1+c4)*(c5/(1-c5))*z[t,1]##( -1-c4)/ (z[t,2]##(-c4));
j = (j11 || j12 ) // (j21 || j22) ;
if any(j = .) then detj = 0.;
else detj = det(j);
if abs(detj) < 1.e-30 then do;
return(.);
end;
lndet = lndet + log(abs(detj));
end;
/* 2. Compute Sigma */
sb = j(2,2,0.);
do t= 1 to 41;
eq_g1 = c1 * 10##(c2 * z[t,4]) * (c5*z[t,1]##(-c4)
+ (1-c5)*z[t,2]##(-c4))##(-c3/c4) - z[t,3];
eq_g2 = (c5/(1-c5)) * (z[t,1] / z[t,2])##(-1-c4) - z[t,5];
resid = eq_g1 // eq_g2;
sb = sb + resid * resid`;
end;
sb = sb / 41;
/* 3. Compute log L */
const = 41. * (log(2 * 3.1415) + 1.);
lnds = 0.5 * 41 * log(det(sb));
logl = const - lndet + lnds;
return(logl);
finish fiml;
There are potential problems in computing the power and log functions for an unrestricted parameter set. As a result, optimization algorithms that use line search fail more often than algorithms that restrict the search area. For that reason, the NLPDD subroutine is used in the following code to maximize the log-likelihood function. Part of the iteration history is shown in Output 15.7.1.
pr = j(1,5,0.001);
optn = {0 2};
tc = {. . . 0};
call nlpdd(rc, xr,"fiml", pr, optn,,tc);
quit;
Output 15.7.1: Iteration History for Two-Equation ML Problem
| Iteration | Restarts | Function Calls |
Active Constraints |
Objective Function |
Objective Function Change |
Max Abs Gradient Element |
Step Size |
Slope of Search Direction |
||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 3 | 1 | -88.51201 | 4.8158 | 16.6594 | 0.0256 | -305.2 | ||
| 2 | 0 | 4 | 1 | -87.42665 | 1.0854 | 10.8769 | 1.000 | -2.157 | ||
| 3 | 0 | 5 | 1 | -87.27408 | 0.1526 | 5.4965 | 1.000 | -0.366 | ||
| 4 | 0 | 7 | 1 | -87.17314 | 0.1009 | 2.2856 | 2.000 | -0.113 | ||
| 5 | 0 | 8 | 1 | -87.16611 | 0.00703 | 0.3444 | 1.000 | -0.0149 | ||
| 6 | 0 | 10 | 1 | -87.16582 | 0.000287 | 0.0522 | 1.001 | -0.0006 | ||
| 7 | 0 | 12 | 1 | -87.16581 | 9.128E-6 | 0.00691 | 1.133 | -161E-7 | ||
| 8 | 0 | 14 | 1 | -87.16581 | 1.712E-7 | 0.00101 | 1.128 | -303E-9 |
The results are very close to those reported by Bard (1974). Bard also reports different approaches to the same problem that can lead to very different MLEs.
Output 15.7.2: Parameter Estimates
| Optimization Results | |||
|---|---|---|---|
| Parameter Estimates | |||
| N | Parameter | Estimate | Gradient Objective Function |
| 1 | X1 | 0.050000 | 40.000241 |
| 2 | X2 | 0.074999 | 40.000622 |
| 3 | X3 | 0.099998 | 40.000887 |
| 4 | X4 | 0.103335 | 39.999422 |
| 5 | X5 | 0.080601 | 39.999337 |
| 6 | X6 | 0.241802 | 39.999631 |
| 7 | X7 | 0.087315 | 40.000599 |
| 8 | X8 | 0.058212 | 39.999533 |
| 9 | X9 | 0.058212 | 39.999533 |
| 10 | X10 | 0.087315 | 40.000599 |
| 11 | X11 | 0.029105 | 40.000082 |
| 12 | X12 | 0.029105 | 40.000082 |