Nonlinear Optimization Examples

Example 15.5 Profile-Likelihood-Based Confidence Intervals

This example calculates confidence intervals based on the profile likelihood for the parameters estimated in the previous example. The following introduction on profile-likelihood methods is based on the paper of Venzon and Moolgavkar (1988).

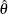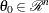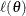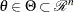Let $\hat{\theta }$ be the maximum likelihood estimate (MLE) of a parameter vector $\theta _0 \in \mathcal{R}^ n$ and let $\ell (\theta )$ be the log-likelihood function defined for parameter values $\theta \in \Theta \subset \mathcal{R}^ n$ .

The profile-likelihood method reduces 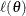$\ell (\theta )$ to a function of a single parameter of interest, 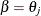$\beta =\theta _ j$ , where 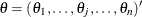$\theta =(\theta _1,\ldots , \theta _ j,\ldots ,\theta _ n)^{\prime }$ , by treating the others as nuisance parameters and maximizing over them. The profile likelihood for 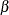$\beta$ is defined as

$\tilde{\ell }_ j(\beta ) = \max _{\theta \in \Theta _ j(\beta )} \ell (\theta )$

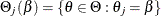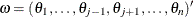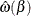where $\Theta _ j(\beta ) = \{ \theta \in \Theta : \theta _ j=\beta \}$ . Define the complementary parameter set $\omega = (\theta _1,\ldots ,\theta _{j-1},\theta _{j+1}, \ldots ,\theta _ n)^{\prime }$ and $\hat{\omega }(\beta )$ as the optimizer of 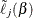$\tilde{\ell }_ j(\beta )$ for each value of 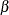$\beta$ . Of course, the maximum of function 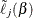$\tilde{\ell }_ j(\beta )$ is located at 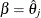$\beta =\hat{\theta }_ j$ . The profile-likelihood-based confidence interval for parameter 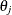$\theta _ j$ is defined as

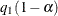$\{ \beta : \ell (\hat{\theta }) - \tilde{\ell }_ j(\beta ) \leq \frac{1}{2}q_1(1-\alpha ) \}$

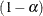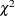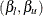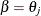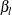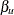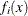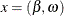where $q_1(1-\alpha )$ is the $(1-\alpha )$ th quantile of the $\chi ^2$ distribution with one degree of freedom. The points $(\beta _ l,\beta _ u)$ are the endpoints of the profile-likelihood-based confidence interval for parameter $\beta =\theta _ j$ . The points $\beta _ l$ and $\beta _ u$ can be computed as the solutions of a system of n nonlinear equations $f_ i(x)$ in n parameters, where $x=(\beta ,\omega )$ :

$\left[ \begin{array}{c} \ell (\theta ) - \ell ^* \\ \frac{\partial \ell }{\partial \omega } (\theta ) \end{array} \right] = 0$

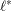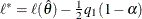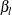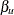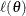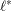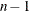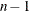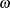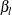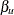where $\ell ^*$ is the constant threshold $\ell ^* = \ell (\hat{\theta }) -\frac{1}{2}q_1(1-\alpha )$ . The first of these n equations defines the locations $\beta _ l$ and $\beta _ u$ where the function $\ell (\theta )$ cuts $\ell ^*$ , and the remaining $n-1$ equations define the optimality of the $n-1$ parameters in $\omega$ . Jointly, the n equations define the locations $\beta _ l$ and $\beta _ u$ where the function 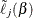$\tilde{\ell }_ j(\beta )$ cuts the constant threshold 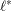$\ell ^*$ , which is given by the roots of 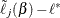$\tilde{\ell }_ j(\beta ) - \ell ^*$ . 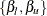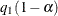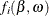Assuming that the two solutions $\{ \beta _ l,\beta _ u\}$ exist (they do not if the quantile $q_1(1-\alpha )$ is too large), this system of n nonlinear equations can be solved by minimizing the sum of squares of the n functions $f_ i(\beta ,\omega )$ :

$F = \frac{1}{2} \sum _{i=1}^ n f_ i^2(\beta ,\omega )$

For a solution of the system of n nonlinear equations to exist, the minimum value of the convex function F must be zero.

The following statements defines the module for the system of 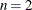$n=2$ nonlinear equations to be solved in terms of the modules that are defined in the previous section:

start f_plwei2(x) global(carcin,ipar,lstar);
   /* use x[1]=sig, x[2]=c, thet */
   like = f_weib2(x);
   grad = g_weib2(x);
   grad[ipar] = like - lstar;
   return(grad`);
finish f_plwei2;

The following statements implements the Levenberg-Marquardt algorithm with the NLPLM subroutine to solve the system of two equations for the left and right endpoints of the interval. The starting point is the optimizer 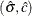$(\hat{\sigma },\hat{c})$ , as computed in the previous example, moved toward the left or right endpoint of the interval by an initial step (refer to Venzon and Moolgavkar (1988)). This forces the algorithm to approach the specified endpoint. The results, shown in Output 15.5.1, are close to the results shown in Output 15.4.2.

/* quantile of chi**2 distribution */
chqua = cinv(1-prob,1); lstar = fopt - .5 * chqua;
/* set number of equations = 2, and print parameter = 0 */
optn = {2 0};                    /* Dont print in NLPLM */
do ipar = 1 to 2;
   /* Compute initial step: */
   /* Choose (alfa,delt) to go in right direction */
   /* Venzon & Moolgavkar (1988), p.89 */
   if ipar=1 then ind = 2; else ind = 1;
   delt = - inv(hes2[ind,ind]) * hes2[ind,ipar];
   alfa = - (hes2[ipar,ipar] - delt` * hes2[ind,ipar]);
   if alfa > 0 then do;
   alfa = .5 * sqrt(chqua / alfa);
   end; else do;
   print "Bad alpha";
   alfa = .1 * xopt[ipar];
   end;
   if ipar=1 then delt = 1 // delt;
           else delt = delt // 1;

   /* Get upper end of interval */
   x0 = xopt + alfa * delt;
   /* set lower bound to optimal value */
   con2 = con; con2[1,ipar] = xopt[ipar];
   CALL NLPLM(rc,xres,"f_plwei2",x0,optn,con2);
   f = f_plwei2(xres); s = ssq(f);
   if (s < 1.e-6) then xub[ipar] = xres[ipar];
                else xub[ipar] = .;

   /* Get lower end of interval */
   x0 = xopt - alfa * delt;
   /* reset lower bound and set upper bound to optimal value */
   con2[1,ipar] = con[1,ipar]; con2[2,ipar] = xopt[ipar];
   CALL NLPLM(rc,xres,"f_plwei2",x0,optn,con2);
   f = f_plwei2(xres); s = ssq(f);
   if (s < 1.e-6) then xlb[ipar] = xres[ipar];
                else xlb[ipar] = .;
end;
results = xlb || xopt || xub;
print results[L="Profile-Likelihood Confidence Interval"
              c={"Lower Bound" "Estimate" "UpperBound"}
              r={"sigma" "c"}];

Output 15.5.1: Confidence Interval Based on Profile Likelihood

Profile-Likelihood Confidence Interval
	Lower Bound	Estimate	UpperBound
sigma	215.1963	234.31861	255.2157
c	4.1344126	6.0831471	8.3063797