Nonlinear Optimization Examples
Example 15.4 MLEs for Two-Parameter Weibull Distribution
This example considers a data set given in Lawless (1982). The data are the number of days it took rats painted with a carcinogen to develop carcinoma. The last two observations are censored. Maximum likelihood estimates (MLEs) and confidence intervals for the parameters of the Weibull distribution are computed. In the following code, the data set is given in the vector CARCIN, and the variables P and M give the total number of observations and the number of uncensored observations. The set D represents the indices of the observations.
proc iml;
carcin = { 143 164 188 188 190 192 206
209 213 216 220 227 230 234
246 265 304 216 244 };
p = ncol(carcin);
m = p - 2;
minx = carcin[><];
rang = carcin[<>] - minx;
The three-parameter Weibull distribution uses three parameters: a scale parameter, a shape parameter, and a location parameter.
This example computes MLEs and corresponding 95% confidence intervals for the scale parameter,  , and the shape parameter, c, for a constant value of the location parameter,
, and the shape parameter, c, for a constant value of the location parameter, 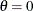 . The program can be generalized to estimate all three parameters. Note that Lawless (1982) denotes
. The program can be generalized to estimate all three parameters. Note that Lawless (1982) denotes  , c, and
, c, and 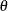 by
by  ,
, 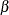 , and
, and 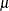 , respectively.
, respectively.
The observed likelihood function of the three-parameter Weibull distribution is
![\[ L(\theta ,\sigma ,c) = \frac{c^ m}{\sigma ^ m} \prod _{i \in D} \left( \frac{t_ i - \theta }{\sigma } \right)^{c-1} \prod _{i=1}^ p \exp \left\{ -\left( \frac{t_ i - \theta }{\sigma } \right)^{c} \right\} \]](images/imlug_nonlinearoptexpls0307.png)
The log likelihood, 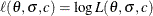 , is
, is
![\[ \ell (\theta ,\sigma ,c) = m \log c - mc \log \sigma + (c-1) \sum _{i \in D} \log (t_ i - \theta ) - \sum _{i=1}^ p \left(\frac{t_ i - \theta }{\sigma }\right)^{c} \]](images/imlug_nonlinearoptexpls0309.png)
The log-likelihood function, 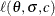 , for
, for 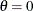 is the objective function to be maximized to obtain the MLEs
is the objective function to be maximized to obtain the MLEs 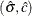 . The following statements define the function:
. The following statements define the function:
/*--- 1. Two parameter estimation: for thet = 0 ---*/ start f_weib2(x) global(carcin,thet); /* use x[1]=sig and x[2]=c */ p = ncol(carcin); m = p - 2; temp = carcin - thet; sum1 = sum(log(temp[1:m])); sum2 = sum((temp / x[1])##x[2]); f = m*log(x[2]) - m*x[2]*log(x[1]) + (x[2]-1)*sum1 - sum2; return(f); finish f_weib2;
The derivatives of 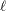 with respect to the parameters
with respect to the parameters 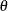 ,
,  , and c are given in Lawless (1982). The following code specifies a gradient module, which computes
, and c are given in Lawless (1982). The following code specifies a gradient module, which computes 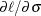 and
and 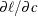 :
:
start g_weib2(x) global(carcin,thet); /* use x[1]=sig and x[2]=c */ p = ncol(carcin); m = p - 2; g = j(1,2,0.); temp = carcin - thet; sum1 = sum(log(temp[1:m])); sum2 = sum((temp / x[1])##x[2]); sum3 = sum(((temp / x[1])##x[2]) # (log(temp / x[1]))); g[1] = -m * x[2] / x[1] + sum2 * x[2] / x[1]; g[2] = m / x[2] - m * log(x[1]) + sum1 - sum3; return(g); finish g_weib2;
The MLEs are computed by maximizing the objective function with the trust-region algorithm in the NLPTR subroutine. The following
code specifies starting values for the two parameters, 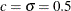 , and to avoid infeasible values during the optimization process, it imposes lower bounds of
, and to avoid infeasible values during the optimization process, it imposes lower bounds of 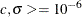 . The optimal parameter values are saved in the variable XOPT, and the optimal objective function value is saved in the variable
FOPT.
. The optimal parameter values are saved in the variable XOPT, and the optimal objective function value is saved in the variable
FOPT.
n = 2; thet = 0.;
x0 = j(1,n,.5);
optn = {1 2};
con = { 1.e-6 1.e-6 ,
. . };
CALL NLPTR(rc,xopt,"f_weib2",x0,optn,con,,,,"g_weib2");
fopt = f_weib2(xopt);
The results shown in Output 15.4.1 are the same as those given in Lawless (1982).
Output 15.4.1: Parameter Estimates for Carcinogen Data
The following code computes confidence intervals based on the asymptotic normal distribution. These are compared with the profile-likelihood-based confidence intervals computed in the next example. The diagonal of the inverse Hessian (as calculated by the NLPFDD subroutine) is used to calculate the standard error.
/*--- Compute confidence interval for x at optimum ---*/
/* compute Hessian at optimum */
xopt = xopt`;
call nlpfdd(f,g,hes2,"f_weib2",xopt,,"g_weib2");
hin2 = inv(hes2);
/* quantile of normal distribution */
prob = 0.05;
stderr = sqrt(abs(vecdiag(hin2)));
z = quantile("Normal", 1 - prob/2);
xlb = xopt - z * stderr;
xub = xopt + z * stderr;
results = xlb || xopt || xub;
print results[L="Normal Distribution Confidence Interval"
c={"Lower Bound" "Estimate" "UpperBound"}
r={"sigma" "c"}];
Output 15.4.2: Confidence Interval Based on Normal Distribution