Language Reference

TSBAYSEA Call

CALL TSBAYSEA (trend, season, series, adjust, abic, data <*>,order <*>, sorder <*>, rigid <*>, npred <*>, opt <*>, cntl <*>, print );

The TSBAYSEA subroutine performs Bayesian seasonal adjustment modeling.

The input arguments to the TSBAYSEA subroutine are as follows:

data

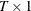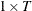specifies a $T \times 1$ (or $1 \times T$ ) data vector.

order

specifies the order of trend differencing. The default is order=2.

sorder

specifies the order of seasonal differencing. The default is sorder=1.

rigid

specifies the rigidity of the seasonal pattern. The default is rigid=1.

npred

specifies the length of the forecast beyond the available observations. The default is npred=0.

opt

specifies the options vector.

opt[1]: specifies the number of seasonal periods (speriod). By default, opt[1]=12.
opt[2]: specifies the year when the series starts (year). If opt[2]=0, there will be no trading day adjustment. By default, opt[2]=0.
opt[3]: specifies the month when the series starts (month). If opt[2]=0, this option is ignored. By default, opt[3]=1.
opt[4]: specifies the upper limit value for outlier determination (rlim). Outliers are considered as missing values. If this value is less than or equal to 0, TSBAYSEA assumes that the input data does not contain outliers. The default is rlim=0. See the section Missing Values.
opt[5]: refers to the number of time periods processed at one time (span). The default is opt[5]=4.
opt[6]: specifies the number of time periods to be shifted (shift). By default, opt[6]=1.
opt[7]: controls the transformation of the original series (logt). If opt[7]=1, log transformation is requested. No transformation (opt[7]=0) is the default.

cntl

specifies control values for the TSBAYSEA subroutine. These values are automatically set. Be careful if you change these values.

cntl[1]: controls the adaptivity of the trading day adjustment component (wtrd). The default is cntl[1]=1.0.
cntl[2]: controls the sum of seasonal components within a period (zersum). The larger the value of cntl[2], the closer to zero this sum is. By default, cntl[2]=1.0.
cntl[3]: controls the leap year effect (delta). The default is cntl[3]=7.0.
cntl[4]: specifies the prior variance of the initial trend (alpha). The default is cntl[4]=0.01.
cntl[5]: specifies the prior variance of the initial seasonal component (beta). The default is cntl[5]=0.01.
cntl[6]: specifies the prior variance of the initial sum of seasonal components (gamma). The default is cntl[6]=0.01.

print

requests the power spectrum and the estimated and forecast values of time series components. If print=2, the spectra of irregular, differenced trend and seasonal series are printed, together with estimates and forecast values. If print=1, only the estimates and forecast values of time series components are printed.

If print=0, printed output is suppressed. The default is print=0.

The TSBAYSEA subroutine returns the following values:

trend: refers to the estimate and forecast of the trend component.
season: refers to the estimate and forecast of the seasonal component.
series: refers to the smoothed and forecast values of the time series.
adjust: refers to the seasonally adjusted series.
abic: refers to the value of ABIC from the final estimates.

The TSBAYSEA subroutine performs Bayesian seasonal adjustments. The smoothness of the trend and seasonal components is controlled by the prior distribution. The Akaike Bayesian information criterion (ABIC) is defined to compare with alternative models. The basic TSBAYSEA procedure processes the block of data in which the length is SPAN*SPERIOD, while the first block of data consists of length (2*SPAN-1)*SPERIOD. The block of data is shifted successively by SHIFT*SPERIOD.

The TSBAYSEA subroutine decomposes the series 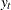$y_ t$ into the following form:

$y_ t = T_ t + S_ t + \epsilon _ t$

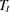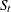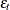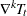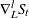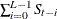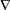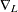where $T_ t$ is a trend component, $S_ t$ denotes a seasonal component, and $\epsilon _ t$ is an irregular component. To estimate the seasonal and trend components, some constraints are imposed such that the sum of squares of $\nabla ^ k T_ t$ , $\nabla ^ l_ L S_ t$ , and $\sum _{i=0}^{L-1} S_{t-i}$ is small, where $\nabla$ and $\nabla _ L$ are difference operators. Then the solution can be obtained by minimizing

$\sum _{t=1}^ N \left\{ (y_ t - T_ t - S_ t)^2 + d^2 \left[ s^2(\nabla ^ k T_ t)^2 + (\nabla ^ l_ L S_ t)^2 + z^2(S_ t + \ldots + S_{t-L+1})^2 \right] \right\}$

where d measures the smoothness of the trend and seasonality, s measures the smoothness of the trend, and z is a smoothness constant for the sum of the seasonal variability. The value of d is estimated while the constants, s and z, are chosen a priori. The value of s is equal to 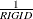$\frac{1}{RIGID}$ , and the constant z is determined as ZERSUM*RIGID/SPERIOD 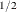$^{1/2}$ . The larger the constant RIGID, the more rigid the seasonal pattern is. See the section Bayesian Constrained Least Squares for more information.

To analyze the monthly data with rigidity 0.5, you can specify either of the following two equivalent statements:

call tsbaysea(trend,season,series,adj,abic) data=z order=2
        sorder=1 rigid=0.5 npred=10 print=2;

call tsbaysea(trend,season,series,adj,abic,z,2,1,0.5,10,,,2);

The TREND, SEASON, and SERIES components contain 10-period-ahead forecast values in addition to the smoothed estimates. The detailed result is also printed since the PRINT=2 option is specified.