Language Reference
SHAPECOL Function
SHAPECOL (matrix, nrow <, ncol> <, pad-value> );
The SHAPECOL function reshapes and repeats values in a matrix. It is similar to the SHAPE function except that the SHAPECOL function produces the result matrix by traversing the argument matrix in column-major order.
The following statements demonstrate the SHAPECOL function:
A = {1 2 3, 4 5 6};
c = shapecol(A, 3);
v = shapecol(A, 0, 1);
print c v;
The vector v in the example is called the "vec of 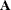 " and is written
" and is written 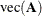 . Uses of the
. Uses of the 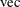 operator in matrix algebra are described in Harville (1997). One important property is the relationship between the
operator in matrix algebra are described in Harville (1997). One important property is the relationship between the 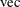 operator and the direct product operator
(Kronecker product operator). If
operator and the direct product operator
(Kronecker product operator). If 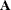 ,
, 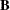 , and
, and 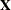 have the appropriate dimensions, then
have the appropriate dimensions, then
![\[ \mbox{vec}(\bA \bX \bB ) = (\bB ^\prime \otimes \bA )\mbox{vec}(\bX ) \]](images/imlug_langref1318.png)
There is also a relationship between the SHAPECOL function and the SHAPE function
. If 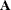 is a matrix, then the following two computations are equivalent:
is a matrix, then the following two computations are equivalent:
b = shapecol(A, m, n, padVal); c = T(shape(A`, n, m, padVal));
See the VECH function for a similar function that is useful for computing with symmetric matrices.