Language Reference
RANDNORMAL Function
RANDNORMAL (N, Mean, Cov );
The RANDNORMAL function is part of the IMLMLIB library
. The RANDNORMAL function returns an 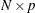 matrix that contains N random draws from the multivariate normal distribution with mean vector Mean and covariance matrix Cov.
matrix that contains N random draws from the multivariate normal distribution with mean vector Mean and covariance matrix Cov.
The inputs are as follows:
- N
-
is the number of desired observations sampled from the multivariate normal distribution.
- Mean
-
is a
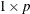 vector of means.
vector of means.
- Cov
-
is a
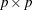 symmetric positive definite variance-covariance matrix.
symmetric positive definite variance-covariance matrix.
If X follows a multivariate normal distribution with mean vector 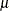 and variance-covariance matrix
and variance-covariance matrix 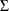 , then
, then
-
the probability density function for x is
![\[ f(x; \mu , \Sigma ) = \frac{1}{(2 \pi )^{p/2} |\Sigma |^{1/2}} \exp \left( - \frac{(x-\mu ) \Sigma ^{-1} (x-\mu )^ T}{2} \right) \]](images/imlug_langref1159.png)
-
if
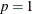 , the probability density function reduces to a univariate normal distribution.
, the probability density function reduces to a univariate normal distribution.
-
the expected value of
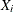 is
is 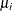 .
.
-
the covariance of
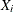 and
and 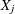 is
is 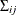 .
.
The following example generates 1,000 samples from a two-dimensional multivariate normal distribution with mean vector 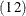 and a given covariance matrix. Each row of the returned matrix
and a given covariance matrix. Each row of the returned matrix x is a row vector sampled from the multivariate normal distribution. The example computes the sample mean and covariance and
compares them with the expected values.
call randseed(1);
N = 1000;
Mean = {1 2};
Cov = {2.4 3, 3 8.1};
x = RandNormal( N, Mean, Cov );
SampleMean = mean(x);
SampleCov = cov(x);
print SampleMean Mean, SampleCov Cov;
Figure 25.307: Estimated Mean and Covariance Matrix
For further details about sampling from the multivariate normal distribution, see Gentle (2003).