Language Reference
RANDDIRICHLET Function
RANDDIRICHLET (N, Shape);
The RANDDIRICHLET function is part of the IMLMLIB library . The RANDDIRICHLET function generates a random sample from a Dirichlet distribution, which is a multivariate generalization of the beta distribution.
The input parameters are as follows:
- N
-
is the number of observations to sample.
- Shape
-
is a
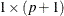 vector of shape parameters for the distribution,
vector of shape parameters for the distribution, ![$\mbox{Shape}[i]>0$](images/imlug_langref1033.png) .
.
The RANDDIRICHLET function returns an 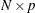 matrix that contains N random draws from the Dirichlet distribution.
matrix that contains N random draws from the Dirichlet distribution.
If 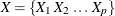 with
with 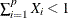 and
and 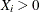 follows a Dirichlet distribution with shape parameter
follows a Dirichlet distribution with shape parameter 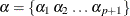 , then
, then
-
the probability density function for x is
![\[ f(x; \alpha ) = \frac{\Gamma (\sum _{i=1}^{p+1}{\alpha _ i})}{\prod _{i=1}^{p+1} \Gamma (\alpha _ i) } \prod _{i=1}^ p { {x_ i}^{\alpha _ i -1}(1-x_1-x_2- \ldots -x_ p)^{\alpha _{p+1}-1} } \]](images/imlug_langref1039.png)
-
if
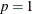 , the probability distribution is a beta distribution.
, the probability distribution is a beta distribution.
-
if
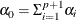 , then
, then
-
the expected value of
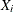 is
is 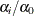 .
.
-
the variance of
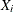 is
is 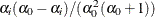 .
.
-
the covariance of
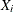 and
and 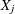 is
is 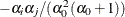 .
.
-
The following example generates 1,000 samples from a two-dimensional Dirichlet distribution. Each row of the returned matrix
x is a row vector sampled from the Dirichlet distribution. The following example computes the sample mean and covariance and
compares them with the expected values:
call randseed(1);
n = 1000;
Shape = {2, 1, 1};
x = RandDirichlet(n,Shape);
d = nrow(Shape)-1;
s = Shape[1:d];
Shape0 = sum(Shape);
Mean = s`/Shape0;
Cov = -s*s` / (Shape0##2*(Shape0+1));
/* replace diagonal elements with variance */
Variance = s#(Shape0-s) / (Shape0##2*(Shape0+1));
do i = 1 to d;
Cov[i,i] = Variance[i];
end;
SampleMean = mean(x);
SampleCov = cov(x);
print SampleMean Mean, SampleCov Cov;
Figure 25.301: Estimated Mean and Covariance Matrix
For further details about sampling from the Dirichlet distribution, see Kotz, Balakrishnan, and Johnson (2000); Gentle (2003); or Devroye (1986).