Language Reference
HOMOGEN Function
HOMOGEN (matrix);
The HOMOGEN function solves the homogeneous system of linear equations 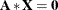 for
for 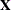 . For at least one solution vector
. For at least one solution vector 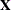 to exist, the
to exist, the  matrix
matrix 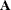 ,
, 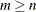 , has to be of rank
, has to be of rank 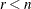 . The HOMOGEN function computes an
. The HOMOGEN function computes an 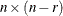 column orthonormal matrix
column orthonormal matrix 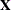 with the properties that
with the properties that 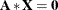 and
and 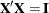 . In other words, the columns of
. In other words, the columns of 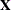 form an orthonormal basis for the nullspace of A.
form an orthonormal basis for the nullspace of A.
If 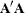 is ill-conditioned, rounding-error problems can occur in determining the correct rank of
is ill-conditioned, rounding-error problems can occur in determining the correct rank of 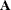 and in determining the correct number of solutions
and in determining the correct number of solutions 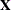 .
.
The following statements compute an example from Wilkinson and Reinsch (1971):
a = {22 10 2 3 7,
14 7 10 0 8,
-1 13 -1 -11 3,
-3 -2 13 -2 4,
9 8 1 -2 4,
9 1 -7 5 -1,
2 -6 6 5 1,
4 5 0 -2 2};
x = homogen(a);
print x;
Figure 25.163: Solutions to a Homogeneous System
In addition, you can use the HOMOGEN function to determine the rank of an  matrix
matrix 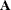 where
where 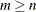 by counting the number of columns in the matrix
by counting the number of columns in the matrix 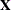 .
.
If A is an 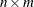 matrix, then, in addition to the memory allocated for the return matrix, the HOMOGEN function temporarily allocates an
matrix, then, in addition to the memory allocated for the return matrix, the HOMOGEN function temporarily allocates an 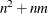 array for performing its computation.
array for performing its computation.