Language Reference
GINV Function
GINV (matrix);
The GINV function computes the Moore-Penrose generalized inverse of matrix. This inverse, known as the four-condition inverse, has these properties:
If  then
then
![\[ \mb{AGA} = \bA ~ ~ ~ \mb{GAG}= \mb{G} ~ ~ ~ (\mb{AG})^{\prime } = \mb{AG} ~ ~ ~ (\mb{GA})^{\prime } = \mb{GA} ~ \]](images/imlug_langref0394.png)
The generalized inverse is also known as the pseudoinverse, usually denoted by  . It is computed by using the singular value decomposition (Wilkinson and Reinsch 1971).
. It is computed by using the singular value decomposition (Wilkinson and Reinsch 1971).
See Rao and Mitra (1971) for a discussion of properties of this function.
As an example, consider the following model:
![\[ \bY = \bX \bbeta + \bepsilon \]](images/imlug_langref0396.png)
Least squares regression for this model can be performed by using the quantity ginv(x)*y as the estimate of  . This solution has minimum
. This solution has minimum  among all solutions that minimize
among all solutions that minimize  , where
, where  .
.
Projection matrices can be formed by specifying GINV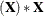 (row space) or
(row space) or  GINV
GINV (column space).
(column space).
The following program demonstrates some common uses of the GINV function:
A = {1 0 1 0 0,
1 0 0 1 0,
1 0 0 0 1,
0 1 1 0 0,
0 1 0 1 0,
0 1 0 0 1 };
/* find generalized inverse */
Ainv = ginv(A);
/* find LS solution: min |Ax-b|^2 */
b = { 3, 2, 4, 2, 1, 3 };
x = Ainv*b;
/* form projection matrix onto row space.
Note P = P` and P*P = P */
P = Ainv*A;
/* find numerical rank of A */
rankA = round(trace(P));
reset fuzz;
print Ainv, rankA, x, P;
Figure 25.146: Common Uses of the Generized Inverse
If 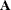 is an
is an 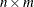 matrix, then, in addition to the memory allocated for the return matrix, the GINV function temporarily allocates an
matrix, then, in addition to the memory allocated for the return matrix, the GINV function temporarily allocates an 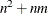 array for performing its computation.
array for performing its computation.