Language Reference
APPCORT Call
CALL APPCORT (prqb, lindep, a, b, <, sing> );
If 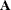 is rank-deficient, then the least squares problem
is rank-deficient, then the least squares problem 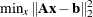 has infinitely many solutions (Golub and Van Loan 1989, p. 241). However, there is a unique solution which has the smallest Euclidean norm. The APPCORT subroutine computes the
minimum Euclidean-norm solution of the (rank-deficient) least squares problem by applyng a complete orthogonal decomposition
by Householder transformations to the vector
has infinitely many solutions (Golub and Van Loan 1989, p. 241). However, there is a unique solution which has the smallest Euclidean norm. The APPCORT subroutine computes the
minimum Euclidean-norm solution of the (rank-deficient) least squares problem by applyng a complete orthogonal decomposition
by Householder transformations to the vector 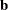 .
.
The input arguments to the APPCORT subroutine are as follows:
- a
-
is an
 matrix
matrix 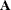 , with
, with 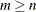 , which is to be decomposed into the product of the
, which is to be decomposed into the product of the  orthogonal matrix
orthogonal matrix 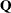 , the
, the 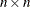 upper triangular matrix
upper triangular matrix 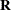 , and the
, and the 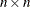 orthogonal matrix
orthogonal matrix 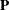 ,
,
![\[ \bA = \bQ \left[ \begin{array}{c} \bR \\ \mb{0} \end{array} \right] \bPi ^{\prime } \bP ^{\prime } \bPi \]](images/imlug_langref0049.png)
- b
-
is a
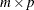 matrix,
matrix, 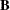 .
.
- sing
-
is an optional scalar that specifies a singularity criterion.
The APPCORT subroutine returns the following values:
- prqb
-
is an
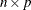 matrix product
matrix product
![\[ \bP \bPi \left[ \begin{array}{cc} (\bL ^{\prime })^{-1} & \mb{0} \\ \mb{0} & \mb{0} \end{array} \right] \bQ ^{\prime } \bB \]](images/imlug_langref0052.png)
which is the minimum Euclidean-norm solution of the rank-deficient least squares problem
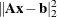 .
.
- lindep
-
is the number of linearly dependent columns in the matrix
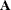 that are detected by applying the r Householder transformations. That is, lindep is
that are detected by applying the r Householder transformations. That is, lindep is  , where r is the numerical rank of
, where r is the numerical rank of 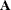 .
.
See the section COMPORT Call for information about complete orthogonal decomposition.
The following example uses the APPCORT call to solve a rank-deficient least squares problem:
/* compute solution for rank-deficient least squares problem:
min |Ax-b|^2
The range of A is a line; b is a point not on the line. */
A = {1 2,
2 4,
-1 -2};
b = {1, 3, -2};
call appcort(x,lindep,A,b);
print x;
The argument b can also be a matrix. If b is an identity matrix, then you can use the APPCORT subroutine to form a generalized inverse, as shown in the following example:
/* A has only four linearly independent columns */
A = {1 0 1 0 0,
1 0 0 1 0,
1 0 0 0 1,
0 1 1 0 0,
0 1 0 1 0,
0 1 0 0 1 };
/* compute Moore-Penrose generalized inverse */
b = i(nrow(A)); /* identity matrix */
call appcort(Ainv, lindep, A, b);
print Ainv;
/* verify generalized inverse conditions (Golub & Van Loan, p. 243) */
eps = 1e-12;
if any(A*Ainv*A-A > eps) |
any(Ainv*A*Ainv-Ainv > eps) |
any((A*Ainv)`-A*Ainv > eps) |
any((Ainv*A)`-Ainv*A > eps) then
msg = "Pseudoinverse conditions not satisfied";
else
msg = "Pseudoinverse conditions satisfied";
print msg;
Figure 25.40: Generalized Inverse