Language Reference

The matrix power operator (**) creates a new matrix that is matrix multiplied by itself scalar times. The matrix argument must be square; scalar must be an integer greater than or equal to 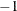. If the scalar is not an integer, it is truncated to an integer.

For example, the following statements compute a matrix that is the result of multiplying a matrix by itself. The result is shown in Figure 25.23.

 a = {1 2,
      1 1};
 c = a**2;
print c;

Note that the expression a**(-1) is shorthand for matrix inversion, as shown by the following statements:

 inv = a**(-1);              /* shorthand for matrix inversion */
 ident = inv * a;
 print inv, ident;

The matrix power operator does not support missing values.

Raising a matrix to a large power can cause numerical precision problems. If the matrix is symmetric, it is preferable to operate on its eigenvalues (see the EIGEN call ) rather than to use the matrix power operator directly on the matrix, as shown in the following example:

 b = {2 1,
      1 1};
 call eigen(lambda, E, b);   /* recall that b = E*diag(lambda)*E` */
 power = 20;
 d = lambda##power;
 a20 = E*diag(d)*E`;         /* a**20 since E`*E = Identity */
 print a20;