General Statistics Examples

A regression model that has a complete quadratic set of regressions across several factors can be processed to yield the estimated critical values that can optimize a response. First, the regression is performed for two variables according to the following model:

The estimates are then divided into a vector of linear coefficients (estimates), 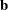, and a matrix of quadratic coefficients, 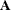. The solution for critical values is

The following program creates a module to perform quadratic response surface regression. For more information about response surface modeling, see the documentation for the RSREG procedure in SAS/STAT User's Guide.

proc iml;
/*          Quadratic Response Surface Regression            */
/* This matrix routine reads in the factor variables and     */
/* the response, forms the quadratic regression model and    */
/* estimates the parameters, and then solves for the optimal */
/* response, prints the optimal factors and response, and    */
/* displays the eigenvalues and eigenvectors of the          */
/* matrix of quadratic parameter estimates to determine if   */
/* the solution is a maximum or minimum, or saddlepoint, and */
/* which direction has the steepest and gentlest slopes.     */
/*                                                           */
/* Given:                                                    */
/* d contains the factor variables                           */
/* y contains the response variable                          */
/*                                                           */

start rsm(d, y);
   n=nrow(d);
   k=ncol(d);                                  /* dimensions */
   x=j(n,1,1) || d;                  /* set up design matrix */
   do i=1 to k;                     /* add quadratic effects */
      x = x || d[,i] #d[,1:i];
   end;
   beta=solve(x`*x, x`*y);            /* estimate parameters */
   names = "b0":("b"+strip(char(nrow(beta)-1)));
   print beta[rowname=names label="Parameter Estimates"];

   c=beta[1];                          /* intercept estimate */
   b=beta[2:(k+1)];                      /* linear estimates */
   a=j(k,k,0);
   L=k+1;                     /* form quadratics into matrix */
   do i=1 to k;
      do j=1 to i;
         L=L+1;
         a[i,j]=beta [L,];
      end;
   end;
   a=(a+a`)/2;                                 /* symmetrize */
   xx = -0.5*solve(a,b);         /* solve for critical value */
   print xx[label="Critical Factor Values"];

   /* Compute response at critical value */
   yopt=c + b`*xx + xx`*a*xx;
   print yopt[label="Response at Critical Value"];

   call eigen(eval,evec,a);
   if min(eval)>0 then print "Solution Is a Minimum";
   if max(eval)<0 then print "Solution Is a Maximum";
finish rsm;

The following statements run the RSM module and use sample data that represent the result of a designed experiment with two factors. The results are shown in Output 10.7.1

/* Sample Problem with Two Factors */
d = {-1 -1, -1  0, -1  1,
      0 -1,  0  0,  0  1,
      1 -1,  1  0,  1  1};
y = {71.7, 75.2, 76.3, 79.2, 81.5, 80.2, 80.1, 79.1, 75.8};
run rsm(d,y);

Output 10.7.1 displays the parameter estimates from the regression and shows that the values 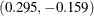are values of the factors that result in a maximum response, based on a quadratic fit of the data. The maximum value of the response is predicted to be about 81.5.