Nonlinear Optimization Examples
The options vector, represented by the "opt" argument, enables you to specify a variety of options, such as the amount of printed output or particular update or line-search techniques. Table 14.2 gives a summary of the available options.
Table 14.2: Summary of the Elements of the Options Vector
|
Index |
Description |
|---|---|
|
1 |
specifies minimization, maximization, or the number of least squares functions |
|
2 |
specifies the amount of printed output |
|
3 |
NLPDD, NLPLM, NLPNRA, NLPNRR, NLPTR: specifies the scaling of the Hessian matrix (HESCAL) |
|
4 |
NLPCG, NLPDD, NLPHQN, NLPQN: specifies the update technique (UPDATE) |
|
5 |
NLPCG, NLPHQN, NLPNRA, NLPQN (with no nonlinear constraints): specifies the line-search technique (LIS) |
|
6 |
NLPHQN: specifies version of hybrid algorithm (VERSION) |
|
NLPQN with nonlinear constraints: specifies version of |
|
|
7 |
NLPDD, NLPHQN, NLPQN: specifies initial Hessian matrix (INHESSIAN) |
|
8 |
Finite-Difference Derivatives: specifies type of differences and how to compute the difference interval |
|
9 |
NLPNRA: specifies the number of rows returned by the sparse Hessian module |
|
10 |
NLPNMS, NLPQN: specifies the total number of constraints returned by the "nlc" module |
|
11 |
NLPNMS, NLPQN: specifies the number of equality constraints returned by the "nlc" module |
The following list contains detailed explanations of the elements of the options vector:
-
opt[1] indicates whether the problem is minimization or maximization. The default, opt
![$[1]=0$](images/imlug_nonlinearoptexpls0129.png) , specifies a minimization problem, and opt
, specifies a minimization problem, and opt![$[1]=1$](images/imlug_nonlinearoptexpls0130.png) specifies a maximization problem. For least squares problems, opt
specifies a maximization problem. For least squares problems, opt![$[1]=m$](images/imlug_nonlinearoptexpls0131.png) specifies the number of functions or observations, which is the number of values returned by the "fun" module. This information is necessary to allocate memory for the return vector of the "fun" module.
specifies the number of functions or observations, which is the number of values returned by the "fun" module. This information is necessary to allocate memory for the return vector of the "fun" module.
-
opt[2] specifies the amount of output printed by the subroutine. The higher the value of opt[2], the more printed output is produced. The following table indicates the specific items printed for each value.
Value of opt[2]
Printed Output
0
No printed output is produced. This is the default.
1
The summaries for optimization start and termination are produced, as well as the iteration history.
2
The initial and final parameter estimates are also printed.
3
The values of the termination criteria and other control parameters are also printed.
4
The parameter vector, x, is also printed after each iteration.
5
The gradient vector, g, is also printed after each iteration.
-
opt[3] selects a scaling for the Hessian matrix,
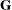 . This option is relevant only for the NLPDD, NLPLM, NLPNRA, NLPNRR, and NLPTR subroutines. If opt
. This option is relevant only for the NLPDD, NLPLM, NLPNRA, NLPNRR, and NLPTR subroutines. If opt![$[3]\ne 0$](images/imlug_nonlinearoptexpls0133.png) , the first iteration and each restart iteration set the diagonal scaling matrix
, the first iteration and each restart iteration set the diagonal scaling matrix 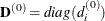 , where
, where
![\[ d_ i^{(0)} = \sqrt {\max (|G^{(0)}_{i,i}|,\epsilon )} \]](images/imlug_nonlinearoptexpls0135.png)
and
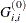 are the diagonal elements of the Hessian matrix, and
are the diagonal elements of the Hessian matrix, and  is the machine precision. The diagonal scaling matrix
is the machine precision. The diagonal scaling matrix 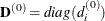 is updated as indicated in the following table.
is updated as indicated in the following table.
Value of opt[3]
Scaling Update
0
No scaling is done.
1
Moré (1978) scaling update:
![\[ d_ i^{(k+1)} = \max \left(d_ i^{(k)}, \sqrt {\max (|G^{(k)}_{i,i}|,\epsilon )}\right) \]](images/imlug_nonlinearoptexpls0137.png)
2
Dennis, Gay, and Welsch (1981) scaling update:
![\[ d_ i^{(k+1)} = \max \left(0.6 * d_ i^{(k)}, \sqrt {\max (|G^{(k)}_{i,i}|,\epsilon )}\right) \]](images/imlug_nonlinearoptexpls0138.png)
3
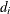 is reset in each iteration:
is reset in each iteration: 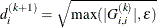
For the NLPDD, NLPNRA, NLPNRR, and NLPTR subroutines, the default is opt
![$[3]=0$](images/imlug_nonlinearoptexpls0141.png) ; for the NLPLM subroutine, the default is opt
; for the NLPLM subroutine, the default is opt![$[3]=1$](images/imlug_nonlinearoptexpls0142.png) .
.
-
opt[4] defines the update technique for (dual) quasi-Newton and conjugate gradient techniques. This option applies to the NLPCG, NLPDD, NLPHQN, and NLPQN subroutines. For the NLPCG subroutine, the following update techniques are available.
Value of opt[4]
Update Method for NLPCG
1
automatic restart method of Powell (1977) and Beale (1972). This is the default.
2
Fletcher-Reeves update (Fletcher, 1987)
3
Polak-Ribiere update (Fletcher, 1987)
4
conjugate-descent update of Fletcher (1987)
For the unconstrained or linearly constrained NLPQN subroutine, the following update techniques are available.
Value of opt[4]
Update Method for NLPQN
1
dual Broyden, Fletcher, Goldfarb, and Shanno (DBFGS) update of the Cholesky factor of the Hessian matrix. This is the default.
2
dual Davidon, Fletcher, and Powell (DDFP) update of the Cholesky factor of the Hessian matrix
3
original Broyden, Fletcher, Goldfarb, and Shanno (BFGS) update of the inverse Hessian matrix
4
original Davidon, Fletcher, and Powell (DFP) update of the inverse Hessian matrix
For the NLPQN subroutine used with the "nlc" module and for the NLPDD and NLPHQN subroutines, only the first two update techniques in the second table are available.
-
opt[5] defines the line-search technique for the unconstrained or linearly constrained NLPQN subroutine, as well as the NLPCG, NLPHQN, and NLPNRA subroutines. Refer to Fletcher (1987) for an introduction to line-search techniques. The following table describes the available techniques.
Value of opt[5]
Line-Search Method
1
This method needs the same number of function and gradient calls for cubic interpolation and cubic extrapolation; it is similar to a method used by the Harwell subroutine library.
2
This method needs more function than gradient calls for quadratic and cubic interpolation and cubic extrapolation; it is implemented as shown in Fletcher (1987) and can be modified to exact line search with the par[6] argument (see the section Control Parameters Vector). This is the default for the NLPCG, NLPNRA, and NLPQN subroutines.
3
This method needs the same number of function and gradient calls for cubic interpolation and cubic extrapolation; it is implemented as shown in Fletcher (1987) and can be modified to exact line search with the par[6] argument.
4
This method needs the same number of function and gradient calls for stepwise extrapolation and cubic interpolation.
5
This method is a modified version of the opt[5]=4 method.
6
This method is the golden section line search of Polak (1971), which uses only function values for linear approximation.
7
This method is the bisection line search of Polak (1971), which uses only function values for linear approximation.
8
This method is the Armijo line-search technique of Polak (1971), which uses only function values for linear approximation.
For the NLPHQN least squares subroutine, the default is a special line-search method that is based on an algorithm developed by Lindström and Wedin (1984). Although it needs more memory, this method sometimes works better with large least squares problems.
-
opt[6] is used only for the NLPHQN subroutine and the NLPQN subroutine with nonlinear constraints.
In the NLPHQN subroutine, it defines the criterion for the decision of the hybrid algorithm to step in a Gauss-Newton or a quasi-Newton search direction. You can specify one of the three criteria that correspond to the methods of Fletcher and Xu (1987). The methods are HY1 (opt[6]=1), HY2 (opt[6]=2), and HY3 (opt[6]=2), and the default is HY2.
In the NLPQN subroutine with nonlinear constraints, it defines the version of the algorithm used to update the vector
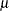 of the Lagrange multipliers. The default is opt[6]=2, which specifies the approach of Powell (1982a) and Powell (1982b). You can specify the approach of Powell (1978a) with opt[6]=1.
of the Lagrange multipliers. The default is opt[6]=2, which specifies the approach of Powell (1982a) and Powell (1982b). You can specify the approach of Powell (1978a) with opt[6]=1.
-
opt[7] defines the type of start matrix,
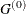 , used for the Hessian approximation. This option applies only to the NLPDD, NLPHQN, and NLPQN subroutines. If opt[7]=0, which is the default, the quasi-Newton algorithm starts with a multiple of the identity matrix where the scalar factor
depends on par[10]; otherwise, it starts with the Hessian matrix computed at the starting point
, used for the Hessian approximation. This option applies only to the NLPDD, NLPHQN, and NLPQN subroutines. If opt[7]=0, which is the default, the quasi-Newton algorithm starts with a multiple of the identity matrix where the scalar factor
depends on par[10]; otherwise, it starts with the Hessian matrix computed at the starting point 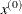 .
.
-
opt[8] defines the type of finite-difference approximation used to compute first- or second-order derivatives and whether the finite-difference intervals, h, should be computed by using an algorithm of Gill et al. (1983). The value of opt[8] is a two-digit integer,
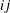 .
.
-
If opt[8] is missing or
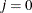 , the fast but not very precise forward difference formulas are used; if
, the fast but not very precise forward difference formulas are used; if 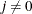 , the numerically more expensive central-difference formulas are used.
, the numerically more expensive central-difference formulas are used.
-
If opt[8] is missing or
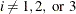 , the finite-difference intervals h are based only on the information of par[8] or par[9], which specifies the number of accurate digits to use in evaluating the objective function and nonlinear constraints,
respectively. If
, the finite-difference intervals h are based only on the information of par[8] or par[9], which specifies the number of accurate digits to use in evaluating the objective function and nonlinear constraints,
respectively. If 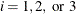 , the intervals are computed with an algorithm by Gill et al. (1983). For
, the intervals are computed with an algorithm by Gill et al. (1983). For 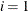 , the interval is based on the behavior of the objective function; for
, the interval is based on the behavior of the objective function; for 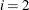 , the interval is based on the behavior of the nonlinear constraint functions; and for
, the interval is based on the behavior of the nonlinear constraint functions; and for 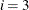 , the interval is based on the behavior of both the objective function and the nonlinear constraint functions.
, the interval is based on the behavior of both the objective function and the nonlinear constraint functions.
The algorithm of Gill et al. (1983) that computes the finite-difference intervals
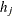 can be very expensive in the number of function calls it uses. If this algorithm is required, it is performed twice, once
before the optimization process starts and once after the optimization terminates. See the section Finite-Difference Approximations of Derivatives for details.
can be very expensive in the number of function calls it uses. If this algorithm is required, it is performed twice, once
before the optimization process starts and once after the optimization terminates. See the section Finite-Difference Approximations of Derivatives for details.
-
opt[9] indicates that the Hessian module "hes" returns a sparse definition of the Hessian, in the form of an
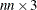 matrix instead of the default dense
matrix instead of the default dense 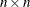 matrix. If opt[9] is zero or missing, the Hessian module must return a dense
matrix. If opt[9] is zero or missing, the Hessian module must return a dense 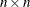 matrix. If you specify opt
matrix. If you specify opt![$[9]=nn$](images/imlug_nonlinearoptexpls0145.png) , the module must return a sparse
, the module must return a sparse 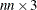 table. See the section Objective Function and Derivatives for more details. This option applies only to the NLPNRA algorithm. If the dense specification contains a large proportion
of analytical zero derivatives, the sparse specification can save memory and computer time.
table. See the section Objective Function and Derivatives for more details. This option applies only to the NLPNRA algorithm. If the dense specification contains a large proportion
of analytical zero derivatives, the sparse specification can save memory and computer time.
-
opt[10] specifies the total number of nonlinear constraints returned by the "nlc" module. If you specify
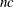 nonlinear constraints with the "nlc" argument module, you must specify opt
nonlinear constraints with the "nlc" argument module, you must specify opt![$[10]=nc$](images/imlug_nonlinearoptexpls0146.png) to allocate memory for the return vector.
to allocate memory for the return vector.
-
opt[11] specifies the number of nonlinear equality constraints returned by the "nlc" module. If the first
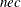 constraints are equality constraints, you must specify opt
constraints are equality constraints, you must specify opt![$[11]=nec$](images/imlug_nonlinearoptexpls0147.png) . The default value is opt
. The default value is opt![$[11]=0$](images/imlug_nonlinearoptexpls0148.png) .
.