Language Reference
CALL NLPHQN (rc, xr, "fun", x0 <*>, opt <*>, blc <*>, tc <*>, par <*>, "ptit" <*>, "jac" );
The NLPHQN subroutine uses a hybrid quasi-Newton least squares method to compute an optimum value of a function.
See the section Nonlinear Optimization and Related Subroutines for a listing of all NLP subroutines. See Chapter 14 for a description of the arguments of NLP subroutines.
The NLPHQN subroutine uses one of the Fletcher and Xu (1987) hybrid quasi-Newton methods. Refer also to Al-Baali and Fletcher (1985) and Al-Baali and Fletcher (1986). In each iteration, the subroutine uses a criterion to decide whether a Gauss-Newton or a dual quasi-Newton search direction is appropriate. You can choose one of three criteria (HY1, HY2, or HY3) proposed by Fletcher and Xu (1987) with the sixth element of the opt vector. The default is HY2. The subroutine computes the crossproduct Jacobian (for the Gauss-Newton step), updates the Cholesky factor of an approximate Hessian (for the quasi-Newton step), and performs a line search to compute an approximate minimum along the search direction. The default line-search technique used by the NLPHQN method is designed for least squares problems ((Lindström and Wedin, 1984) and (Al-Baali and Fletcher, 1986)), but you can specify a different line-search algorithm with the fifth element of the opt argument. See the section Options Vector for details.
You can specify two update formulas with the fourth element of the opt argument as indicated in the following table.
|
Value of opt[4] |
Update Method |
|---|---|
|
1 |
Dual Broyden, Fletcher, Goldfarb, and Shanno (DBFGS) update of the Cholesky factor of the Hessian matrix. This is the default. |
|
2 |
Dual Davidon, Fletcher, and Powell (DDFP) update of the Cholesky factor of the Hessian matrix. |
The NLPHQN subroutine needs approximately the same amount of working memory as the NLPLM subroutine , and in most applications, the latter seems to be superior. Hence, the NLPHQN method is recommended only when the NLPLM method encounters problems.
Note: In least squares subroutines, you must set the first element of the opt vector to m, the number of functions.
In addition to the standard iteration history, the NLPHQN subroutine prints the following information:
-
Under the heading Iter, an asterisk (*) printed after the iteration number indicates that, on the basis of the Fletcher and Xu (1987) criterion, the subroutine used a Gauss-Newton search direction instead of a quasi-Newton search direction.
-
The heading alpha is the step size,
 , computed with the line-search algorithm.
, computed with the line-search algorithm.
-
The heading slope refers to
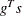 , the slope of the search direction at the current parameter iterate
, the slope of the search direction at the current parameter iterate 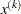 . For minimization, this value should be significantly smaller than zero. Otherwise, the line-search algorithm has difficulty
reducing the function value sufficiently.
. For minimization, this value should be significantly smaller than zero. Otherwise, the line-search algorithm has difficulty
reducing the function value sufficiently.
The following statements use the NLPHQN call to solve the unconstrained Rosenbrock problem (see the section Unconstrained Rosenbrock Function).
title "Test of NLPHQN subroutine: No Derivatives";
start F_ROSEN(x);
y = j(1, 2, 0);
y[1] = 10 * (x[2] - x[1] * x[1]);
y[2] = 1 - x[1];
return(y);
finish F_ROSEN;
x = {-1.2 1};
opt = {2 2};
call nlphqn(rc, xr, "F_ROSEN", x, opt);
Figure 24.237: Optimization Results
| Value of Objective Function = 12.1 |
| Test of NLPHQN subroutine: No Derivatives |
| Hybrid Quasi-Newton LS Minimization |
| Dual Broyden - Fletcher - Goldfarb - Shanno Update (DBFGS) |
| Version HY2 of Fletcher & Xu (1987) |
| Gradient Computed by Finite Differences |
| CRP Jacobian Computed by Finite Differences |
| Parameter Estimates | 2 |
|---|---|
| Functions (Observations) | 2 |
| Iteration | Restarts | Function Calls |
Active Constraints |
Objective Function |
Objective Function Change |
Max Abs Gradient Element |
Step Size |
Slope of Search Direction |
||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 3 | 0 | 7.22423 | 4.8758 | 56.9322 | 0.0616 | -628.8 | ||
| 2 | * | 0 | 5 | 0 | 0.97090 | 6.2533 | 2.3017 | 0.266 | -14.448 | |
| 3 | * | 0 | 7 | 0 | 0.81911 | 0.1518 | 3.7839 | 0.119 | -1.942 | |
| 4 | 0 | 9 | 0 | 0.69103 | 0.1281 | 5.5103 | 2.000 | -0.144 | ||
| 5 | 0 | 19 | 0 | 0.47345 | 0.2176 | 8.8638 | 11.854 | -0.194 | ||
| 6 | * | 0 | 21 | 0 | 0.35906 | 0.1144 | 9.8734 | 0.253 | -0.947 | |
| 7 | * | 0 | 22 | 0 | 0.23342 | 0.1256 | 10.1490 | 0.398 | -0.718 | |
| 8 | * | 0 | 24 | 0 | 0.14799 | 0.0854 | 11.6248 | 1.346 | -0.467 | |
| 9 | * | 0 | 26 | 0 | 0.00948 | 0.1385 | 2.6275 | 1.443 | -0.296 | |
| 10 | * | 0 | 28 | 0 | 1.98834E-6 | 0.00947 | 0.00609 | 0.938 | -0.0190 | |
| 11 | * | 0 | 30 | 0 | 7.0768E-10 | 1.988E-6 | 0.000748 | 1.003 | -398E-8 | |
| 12 | * | 0 | 32 | 0 | 2.0246E-21 | 7.08E-10 | 1.82E-10 | 1.000 | -14E-10 |