QR Call
CALL QR (q, r, piv, lindep, a <, ord> <, b> ) ;
The QR subroutine produces the QR decomposition of a matrix by using Householder transformations.
The QR subroutine returns the following values:
- q
-
specifies an orthogonal matrix
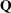 that is the product of the Householder transformations applied to the
that is the product of the Householder transformations applied to the  matrix
matrix 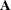 , if the b argument is not specified. In this case, the
, if the b argument is not specified. In this case, the 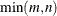 Householder transformations are applied, and q is an
Householder transformations are applied, and q is an  matrix. If the b argument is specified, q is the
matrix. If the b argument is specified, q is the 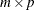 matrix
matrix 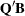 that has the transposed Householder transformations
that has the transposed Householder transformations 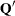 applied on the
applied on the 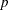 columns of the argument matrix
columns of the argument matrix 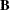 .
.
- r
-
specifies a
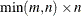 upper triangular matrix
upper triangular matrix 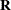 that is the upper part of the
that is the upper part of the  upper triangular matrix
upper triangular matrix 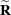 of the QR decomposition of the matrix
of the QR decomposition of the matrix 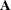 . The matrix
. The matrix 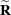 of the QR decomposition can be obtained by vertical concatenation (by using the operator //) of the
of the QR decomposition can be obtained by vertical concatenation (by using the operator //) of the 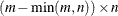 zero matrix to the result matrix
zero matrix to the result matrix 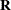 .
.
- piv
-
specifies an
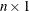 vector of permutations of the columns of
vector of permutations of the columns of 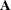 ; that is, on return, the QR decomposition is computed, not of
; that is, on return, the QR decomposition is computed, not of 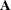 , but of the permuted matrix whose columns are
, but of the permuted matrix whose columns are ![$[\mathbf{A}_{piv[1]} \ldots \mathbf{A}_{piv[n]}]$](images/imlug_langref1197.png) . The vector piv corresponds to an
. The vector piv corresponds to an 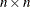 permutation matrix
permutation matrix 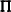 .
.
- lindep
-
is the number of linearly dependent columns in matrix
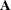 detected by applying the
detected by applying the 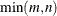 Householder transformations in the order specified by the argument vector piv.
Householder transformations in the order specified by the argument vector piv.
The input arguments to the QR subroutine are as follows:
- a
-
specifies an
 matrix
matrix 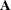 that is to be decomposed into the product of the orthogonal matrix
that is to be decomposed into the product of the orthogonal matrix 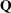 and the upper triangular matrix
and the upper triangular matrix 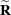 .
.
- ord
-
specifies an optional
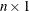 vector that specifies the order of Householder transformations applied to matrix
vector that specifies the order of Householder transformations applied to matrix 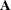 . When you specify the ord argument, the columns of
. When you specify the ord argument, the columns of 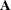 can be divided into the following groups:
can be divided into the following groups:
- ord[j]>0
-
Column
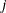 of
of 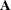 is an initial column, meaning it has to be processed at the start in increasing order of ord[j]. This specification defines the first
is an initial column, meaning it has to be processed at the start in increasing order of ord[j]. This specification defines the first 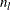 columns of
columns of 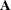 that are to be processed.
that are to be processed.
- ord[j]=0
-
Column
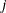 of
of 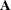 is a pivot column, meaning it is to be processed in order of decreasing residual Euclidean norms. The pivot columns of
is a pivot column, meaning it is to be processed in order of decreasing residual Euclidean norms. The pivot columns of 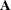 are processed after the
are processed after the 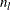 initial columns and before the
initial columns and before the 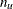 final columns.
final columns.
- ord[j]<0
-
Column
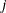 of
of 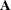 is a final column, meaning it has to be processed at the end in decreasing order of ord[j]. This specification defines the last
is a final column, meaning it has to be processed at the end in decreasing order of ord[j]. This specification defines the last 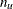 columns of
columns of 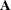 that are to be processed. If
that are to be processed. If 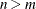 , some of these columns are not processed.
, some of these columns are not processed.
The default is ord[j]=j, in which case the Householder transformations are processed in the same order in which the columns are stored in matrix
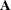 (without pivoting).
(without pivoting).
- b
-
specifies an optional
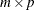 matrix
matrix 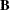 that is to be multiplied by the transposed
that is to be multiplied by the transposed  matrix
matrix 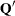 . If b is specified, the result q contains the
. If b is specified, the result q contains the 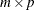 matrix
matrix 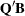 . If b is not specified, the result q contains the
. If b is not specified, the result q contains the  matrix
matrix 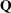 .
.
The QR subroutine decomposes an ![]() matrix
matrix ![]() into the product of an
into the product of an ![]() orthogonal matrix
orthogonal matrix ![]() and an
and an ![]() upper triangular matrix
upper triangular matrix ![]() , so that
, so that
|
|
by means of ![]() Householder transformations.
Householder transformations.
The ![]() orthogonal matrix
orthogonal matrix ![]() is computed only if the last argument b is not specified, as in the following example:
is computed only if the last argument b is not specified, as in the following example:
call qr(q, r, piv, lindep, a, ord);
In many applications, the number of rows, ![]() , is very large. In these cases, the explicit computation of the
, is very large. In these cases, the explicit computation of the ![]() matrix
matrix ![]() might require too much memory or time.
might require too much memory or time.
In the usual case where ![]() ,
,
![$\displaystyle \bA = \left[ \begin{array}{ccc} * & * & * \\ \mbox{}* & * & * \\ \mbox{}* & * & * \\ \mbox{}* & * & * \\ \mbox{}* & * & * \end{array} \right] $](images/imlug_langref1202.png) |
|
![$\displaystyle \bQ = \left[ \begin{array}{ccccc} * & * & * & * & * \\ \mbox{}* & * & * & * & * \\ \mbox{}* & * & * & * & * \\ \mbox{}* & * & * & * & * \\ \mbox{}* & * & * & * & * \end{array} \right] $](images/imlug_langref1204.png) |
![$\displaystyle \widetilde{\bR } = \left[ \begin{array}{ccc} * & * & * \\ 0 & * & * \\ 0 & 0 & * \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right] $](images/imlug_langref1205.png) |
|
![$\displaystyle \bR = \left[\begin{array}{ccc} * & * & * \\ 0 & * & * \\ 0 & 0 & * \end{array} \right] $](images/imlug_langref1206.png) |
|
|
|
|
where ![]() is the result returned by the QR subroutine.
is the result returned by the QR subroutine.
The ![]() columns of matrix
columns of matrix ![]() provide an orthonormal basis for the
provide an orthonormal basis for the ![]() columns of
columns of ![]() and are called the range space of
and are called the range space of ![]() . Since the
. Since the ![]() columns of
columns of ![]() are orthogonal to the
are orthogonal to the ![]() columns of
columns of ![]() ,
, ![]() , they provide an orthonormal basis for the orthogonal complement of the columns of
, they provide an orthonormal basis for the orthogonal complement of the columns of ![]() and are called the null space of
and are called the null space of ![]() .
.
In the case where ![]() ,
,
![$\displaystyle \bA = \left[ \begin{array}{ccccc} * & * & * & * & * \\ \mbox{}* & * & * & * & * \\ \mbox{}* & * & * & * & * \end{array} \right] $](images/imlug_langref1213.png) |
|
![$\displaystyle \bQ = \left[ \begin{array}{ccc} * & * & * \\ \mbox{}* & * & * \\ \mbox{}* & * & * \end{array} \right] $](images/imlug_langref1215.png) |
![$\displaystyle \widetilde{\bR } = \bR = \left[ \begin{array}{ccccc} * & * & * & * & * \\ 0 & * & * & * & * \\ 0 & 0 & * & * & * \end{array} \right] $](images/imlug_langref1216.png) |
Specifying the argument ord as an ![]() vector lets you specify a special order of the columns in matrix
vector lets you specify a special order of the columns in matrix ![]() on which the Householder transformations are applied. There are two special cases:
on which the Householder transformations are applied. There are two special cases:
-
If you do not specify the ord argument, the default values ord
![$[j] = j$](images/imlug_langref1217.png) are used. In this case, Householder transformations are done in the same order in which the columns are stored in
are used. In this case, Householder transformations are done in the same order in which the columns are stored in 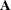 (without pivoting).
(without pivoting).
-
If you set all components of ord to zero, the Householder transformations are done in order of decreasing Euclidean norms of the columns of
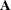 .
.
To check the QR decomposition, use the following statements to compute the three residual sum of squares (represented by the variables SS0, SS1, and SS2), which should be close to zero:
a = shape(1:20, 5); m = nrow(a); n = ncol(a); ord = j(1, n, 0); call qr(q, r, piv, lindep, a); ss0 = ssq(a[ ,piv] - q[,1:n] * r); ss1 = ssq(q * q` - i(m)); ss2 = ssq(q` * q - i(m)); print ss0 ss1 ss2;
Figure 23.247: Result of a QR Decomposition
| ss0 | ss1 | ss2 |
|---|---|---|
| 6.231E-28 | 2.948E-31 | 2.862E-31 |
If the QR subroutine detects linearly dependent columns while processing matrix ![]() , the column order given in the result vector piv can differ from an explicitly specified order in the argument vector ord. If a column of
, the column order given in the result vector piv can differ from an explicitly specified order in the argument vector ord. If a column of ![]() is found to be linearly dependent on columns already processed, this column is swapped to the end of matrix
is found to be linearly dependent on columns already processed, this column is swapped to the end of matrix ![]() . The order of columns in the result matrix
. The order of columns in the result matrix ![]() corresponds to the order of columns processed in
corresponds to the order of columns processed in ![]() . The swapping of a linearly dependent column of
. The swapping of a linearly dependent column of ![]() to the end of the matrix corresponds to the swapping of the same column in
to the end of the matrix corresponds to the swapping of the same column in ![]() and leads to a zero row at the end of the upper triangular matrix
and leads to a zero row at the end of the upper triangular matrix ![]() .
.
The scalar result lindep counts the number of linearly dependent columns that are detected in constructing the first ![]() Householder transformations in the order specified by the argument vector ord. The test of linear dependence depends on the singularity criterion, which is 1E
Householder transformations in the order specified by the argument vector ord. The test of linear dependence depends on the singularity criterion, which is 1E![]() 8 by default.
8 by default.
Solving the linear system ![]() with an upper triangular matrix
with an upper triangular matrix ![]() whose columns are permuted corresponding to the result vector piv leads to a solution
whose columns are permuted corresponding to the result vector piv leads to a solution ![]() with permuted components. You can reorder the components of
with permuted components. You can reorder the components of ![]() by using the index vector piv at the left-hand side of an expression, as follows:
by using the index vector piv at the left-hand side of an expression, as follows:
a = {3 0 0 -1,
0 1 2 0,
4 -4 -1 1,
-1 2 3 4};
b = {-1, 8, -3, 28};
n = ncol(a); p = ncol(b);
ord = j(1, n, 0);
call qr(qtb, r, piv, lindep, a, ord, b);
print piv;
x = j(n,1);
x[piv] = inv(r) * qtb[1:n, 1:p];
print x;
Figure 23.248: Solution to a Linear System
| piv | |||
|---|---|---|---|
| 1 | 4 | 2 | 3 |
| x |
|---|
| 1 |
| 2 |
| 3 |
| 4 |
The Full-Rank Linear Least Squares Problem
This example solves the full-rank linear least squares problem. Specify the argument b as an ![]() matrix
matrix ![]() , as follows:
, as follows:
call qr(q, r, piv, lindep, a, ord, b);
When you specify the b argument, the QR subroutine computes the matrix ![]() (instead of
(instead of ![]() ) as the result q. Now you can compute the
) as the result q. Now you can compute the ![]() least squares solutions
least squares solutions ![]() of an overdetermined linear system with an
of an overdetermined linear system with an ![]() coefficient matrix
coefficient matrix ![]() , rank(
, rank(![]() ) =
) = ![]() , and
, and ![]() right-hand sides b
right-hand sides b![]() stored as the columns of the
stored as the columns of the ![]() matrix
matrix ![]() :
:
|
|
where ![]() is the Euclidean vector norm. This is accomplished by solving the
is the Euclidean vector norm. This is accomplished by solving the ![]() upper triangular systems with back substitution:
upper triangular systems with back substitution:
|
|
For most applications, the number of rows of ![]() ,
, ![]() , is much larger than
, is much larger than ![]() , the number of columns of
, the number of columns of ![]() , or
, or ![]() , the number of right-hand sides. In these cases, you are advised not to compute the large
, the number of right-hand sides. In these cases, you are advised not to compute the large ![]() matrix
matrix ![]() (which can consume too much memory and time) if you can solve your problem by computing only the smaller
(which can consume too much memory and time) if you can solve your problem by computing only the smaller ![]() matrix
matrix ![]() implicitly.
implicitly.
For example, use the first five columns of the ![]() Hilbert matrix
Hilbert matrix ![]() , as follows:
, as follows:
a= { 36 -630 3360 -7560 7560 -2772,
-630 14700 -88200 211680 -220500 83160,
3360 -88200 564480 -1411200 1512000 -582120,
-7560 211680 -1411200 3628800 -3969000 1552320,
7560 -220500 1512000 -3969000 4410000 -1746360,
-2772 83160 -582120 1552320 -1746360 698544 };
aa = a[, 1:5];
b= { 463, -13860, 97020, -258720, 291060, -116424};
m = nrow(aa); n = ncol(aa); p = ncol(b);
call qr(qtb, r, piv, lindep, aa, , b);
if lindep=0 then do;
x=inv(r)*qtb[1:n];
print x; /* x solves aa*x=b */
end;
else /* handle linear dependence */;
Figure 23.249: Solution to Least Squares Problem
| x |
|---|
| 1 |
| 0.5 |
| 0.3333333 |
| 0.25 |
| 0.2 |
Note that you are using only the first ![]() rows,
rows, ![]() , of the
, of the qtb matrix. The IF-THEN statement of the preceding example can be replaced by the more efficient TRISOLV function:
if lindep=0 then x = trisolv(1, r, qtb[1:n], piv);
For information about solving rank-deficient linear least squares problems, see the RZLIND call.