LTS Call :: SAS/IML(R) 12.1 User's Guide

LTS Call

Example

CALL LTS (sc, coef, wgt, opt, y <*>, x <*>, sorb ) ;

The LTS subroutine performs least trimmed squares (LTS) robust regression by minimizing the sum of the smallest squared residuals. The subroutine also detects outliers and perform a least squares regression on the remaining observations. The LTS subroutine implements the FAST-LTS algorithm described by Rousseeuw and Van Driessen (1998).

The value of can be specified, but for many applications the default value works well and the results seem to be quite stable toward different choices of .

In the following discussion, is the number of observations and is the number of regressors. The input arguments to the LTS subroutine are as follows:

opt

specifies an options vector. The options vector can be a vector of missing values, which results in default values for all options. The components of opt are as follows:

opt[1]

specifies whether an intercept is used in the model (opt[1]=0) or not (opt[1] 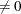$\neq 0$ ). If opt[1]=0, then a column of ones is added as the last column to the input matrix 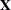$\mb {X}$ ; that is, you do not need to add this column of ones yourself. The default is opt[1]=0.

opt[2]

specifies the amount of printed output. Higher values request additional output and include the output of lower values.

0: prints no output except error messages.
1: prints all output except (1) arrays of 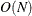, such as weights, residuals, and diagnostics; (2) the history of the optimization process; and (3) subsets that result in singular linear systems.
2: additionally prints arrays of 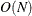, such as weights, residuals, and diagnostics; it also prints the case numbers of the observations in the best subset and some basic history of the optimization process.
3: additionally prints subsets that result in singular linear systems.

The default is opt[2]=0.

opt[3]

specifies whether only LTS is computed or whether, additionally, least squares (LS) and weighted least squares (WLS) regression are computed:

0: computes only LTS.
1: computes, in addition to LTS, weighted least squares regression on the observations with small LTS residuals (where small is defined by opt[8]).
2: computes, in addition to LTS, unweighted least squares regression.
3: adds both unweighted and weighted least squares regression to LTS regression.

The default is opt[3]=0.

opt[4]

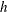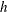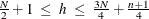specifies the quantile to be minimized. This is used in the objective function. The default is opt[4] $=h=\left[\frac{N+n+1}{2}\right]$ , which corresponds to the highest possible breakdown value. This is also the default of the PROGRESS program. The value of should be in the range $\frac{N}{2}+1 ~ \leq ~ h ~ \leq ~ \frac{3N}{4} + \frac{n+1}{4}$ .

opt[5]

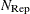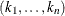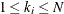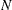specifies the number $N_\mr {Rep}$ of generated subsets. Each subset consists of observations $(k_1,\ldots ,k_ n)$ , where $1 \leq k_ i \leq N$ . The total number of subsets that contain observations out of observations is

$N_\mr {tot} = {N \choose n} = \frac{\prod _{j=1}^ n (N-j+1)}{\prod _{j=1}^ n j}$

where is the number of parameters including the intercept.

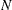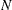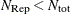Due to computer time restrictions, not all subset combinations of observations out of can be inspected for larger values of and . Specifying a value of $N_\mr {Rep} < N_\mr {tot}$ enables you to save computer time at the expense of computing a suboptimal solution.

When opt[5] is zero or missing:

If 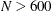, the default FAST-LTS algorithm constructs up to five disjoint random subsets with sizes as equal as possible, but not to exceed 300. Inside each subset, the algorithm chooses 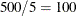subset combinations of observations.

The number of subsets is taken from the following table:

n	1	2	3	4	5	6	7	8	9	10
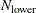
$N_\mr {lower}$	500	50	22	17	15	14	0	0	0	0
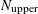
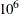
$N_\mr {upper}$		1414	182	71	43	32	27	24	23	22
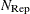
$N_\mr {Rep}$	500	1000	1500	2000	2500	3000	3000	3000	3000	3000

n	11	12	13	14	15
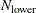
$N_\mr {lower}$	0	0	0	0	0
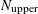
$N_\mr {upper}$	22	22	22	23	23
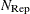
$N_\mr {Rep}$	3000	3000	3000	3000	3000

If the number of cases (observations) 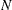is smaller than 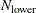$N_\mr {lower}$ , then all possible subsets are used; otherwise, fixed 500 subsets for FAST-LTS or 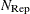$N_\mr {Rep}$ subsets for algorithm before SAS/IML 8.1 are chosen randomly. This means that an exhaustive search is performed for opt[5]=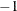. If 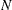is larger than 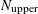$N_\mr {upper}$ , a note is printed in the log file that indicates how many subsets exist.

opt[6]

is not used.

opt[7]

specifies whether the last argument sorb contains a given parameter vector 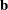$\mb {b}$ or a given subset for which the objective function should be evaluated.

0

sorb contains a given subset index.

1

sorb contains a given parameter vector $\mb {b}$ .

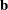The default is opt[7]=0.

opt[8]

is relevant only for LS and WLS regression (opt[3] > 0). It specifies whether the covariance matrix of parameter estimates and approximate standard errors (ASEs) are computed and printed.

0: does not compute covariance matrix and ASEs.
1: computes covariance matrix and ASEs but prints neither of them.
2: computes the covariance matrix and ASEs but prints only the ASEs.
3: computes and prints both the covariance matrix and the ASEs.

The default is opt[8]=0.

opt[9]

is relevant only for LTS. If opt[9]=0, the algorithm FAST-LTS of Rousseeuw and Van Driessen (1998) is used. If opt[9] = 1, the algorithm of Rousseeuw and Leroy (1987) is used. The default is opt[9]=0.

y

a response vector with 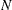observations.

x

an 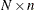$N \times n$ matrix 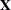$\mb {X}$ of regressors. If opt[1] is zero or missing, an intercept 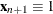$\mb {x}_{n+1} \equiv 1$ is added by default as the last column of 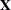$\mb {X}$ . If the matrix 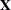$\mb {X}$ is not specified, 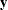$\mb {y}$ is analyzed as a univariate data set.

sorb

refers to an vector that contains either of the following:

observation numbers of a subset for which the objective function should be evaluated; this subset can be the start for a pairwise exchange algorithm if opt[7] is specified.
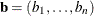given parameters $\mb {b}=(b_1,\ldots ,b_ n)$ (including the intercept, if necessary) for which the objective function should be evaluated.

Missing values are not permitted in or . Missing values in opt cause the default value to be used.

The LTS subroutine returns the following values:

sc

is a column vector that contains the following scalar information, where rows 1–9 correspond to LTS regression and rows 11–14 correspond to either LS or WLS:

sc[1]: the quantile 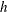used in the objective function
sc[2]: number of subsets generated
sc[3]: number of subsets with singular linear systems
sc[4]: number of nonzero weights
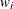
sc[5]: lowest value of the objective function 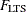$F_\mr {LTS}$ attained
sc[6]: preliminary LTS scale estimate
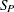
sc[7]: final LTS scale estimate
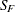
sc[8]: robust R square (coefficient of determination)
sc[9]: asymptotic consistency factor

If opt[3] > 0, then the following are also set:

sc[11]: LS or WLS objective function (sum of squared residuals)
sc[12]: LS or WLS scale estimate
sc[13]: R square value for LS or WLS
sc[14]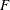: value for LS or WLS

For opt[3]=1 or opt[3]=3, these rows correspond to WLS estimates; for opt[3]=2, these rows correspond to LS estimates.

coef

is a matrix with columns that contains the following results in its rows:

coef[1,]: LTS parameter estimates
coef[2,]: indices of observations in the best subset

If opt[3] > 0, then the following are also set:

coef[3,]: LS or WLS parameter estimates
coef[4,]: approximate standard errors of LS or WLS estimates
coef[5,]: values
coef[6,]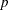: -values
coef[7,]: lower boundary of Wald confidence intervals
coef[8,]: upper boundary of Wald confidence intervals

For opt[3]=1 or opt[3]=3, these rows correspond to WLS estimates; for opt[3]=2, these rows correspond to LS estimates.

wgt

is a matrix with 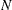columns that contains the following results in its rows:

wgt[1,]: weights (1 for small residuals; 0 for large residuals)
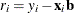
wgt[2,]: residuals $r_ i = y_ i - \mb {x}_ i \mb {b}$
wgt[3,]: resistant diagnostic 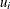(the resistant diagnostic cannot be computed for a perfect fit when the objective function is zero or nearly zero)

Example

Consider Brownlee (1965) stackloss data used in the example for the LMS subroutine.

For and (three explanatory variables including intercept), you obtain a total of 5,985 different subsets of 4 observations out of 21. If you decide not to specify opt[5], the FAST-LTS algorithm chooses random sample subsets, as in the following statements:

   /* X1  X2  X3   Y  Stackloss data */
aa = { 1  80  27  89  42,
       1  80  27  88  37,
       1  75  25  90  37,
       1  62  24  87  28,
       1  62  22  87  18,
       1  62  23  87  18,
       1  62  24  93  19,
       1  62  24  93  20,
       1  58  23  87  15,
       1  58  18  80  14,
       1  58  18  89  14,
       1  58  17  88  13,
       1  58  18  82  11,
       1  58  19  93  12,
       1  50  18  89   8,
       1  50  18  86   7,
       1  50  19  72   8,
       1  50  19  79   8,
       1  50  20  80   9,
       1  56  20  82  15,
       1  70  20  91  15 };

a = aa[, 2:4]; b = aa[, 5];
opt = j(8, 1, .);
opt[2]= 1;    /* ipri */
opt[3]= 3;    /* ilsq */
opt[8]= 3;    /* icov */

call lts(sc, coef, wgt, opt, b, a);

Figure 23.176: Least Trimmed Squares

LTS: The sum of the 13 smallest squared residuals will be minimized.

Median and Mean
	Median	Mean
VAR1	58	60.428571429
VAR2	20	21.095238095
VAR3	87	86.285714286
Intercep	1	1
Response	15	17.523809524

Dispersion and Standard Deviation
	Dispersion	StdDev
VAR1	5.930408874	9.1682682584
VAR2	2.965204437	3.160771455
VAR3	4.4478066555	5.3585712381
Intercep	0	0
Response	5.930408874	10.171622524

Unweighted Least-Squares Estimation

LS Parameter Estimates
Variable	Estimate	Approx Std Err	t Value	Pr > \|t\|	Lower WCI	Upper WCI
VAR1	0.7156402	0.13485819	5.31	<.0001	0.45132301	0.97995739
VAR2	1.29528612	0.36802427	3.52	0.0026	0.57397182	2.01660043
VAR3	-0.1521225	0.15629404	-0.97	0.3440	-0.4584532	0.15420818
Intercep	-39.919674	11.8959969	-3.36	0.0038	-63.2354	-16.603949

Sum of Squares = 178.8299616

Degrees of Freedom = 17

LS Scale Estimate = 3.2433639182

Cov Matrix of Parameter Estimates
	VAR1	VAR2	VAR3	Intercep
VAR1	0.0181867302	-0.036510675	-0.007143521	0.2875871057
VAR2	-0.036510675	0.1354418598	0.0000104768	-0.651794369
VAR3	-0.007143521	0.0000104768	0.024427828	-1.676320797
Intercep	0.2875871057	-0.651794369	-1.676320797	141.51474107

R-squared = 0.9135769045

F(3,17) Statistic = 59.9022259

Probability = 3.0163272E-9

Least Trimmed Squares (LTS) Method

Minimizing Sum of 13 Smallest Squared Residuals.

Highest Possible Breakdown Value = 42.86 %

Random Selection of 517 Subsets

Among 517 subsets 17 is/are singular.

The best half of the entire data set obtained after full iteration consists of the cases:

Estimated Coefficients
VAR1	VAR2	VAR3	Intercep
0.7409210642	0.3915267228	0.0111345398	-37.32332647

LTS Objective Function = 0.474940583

Preliminary LTS Scale = 0.9888435617

Robust R Squared = 0.9745520119

Final LTS Scale = 1.0360272594

Weighted Least-Squares Estimation

RLS Parameter Estimates Based on LTS
Variable	Estimate	Approx Std Err	t Value	Pr > \|t\|	Lower WCI	Upper WCI
VAR1	0.75694055	0.07860766	9.63	<.0001	0.60287236	0.91100874
VAR2	0.45353029	0.13605033	3.33	0.0067	0.18687654	0.72018405
VAR3	-0.05211	0.05463722	-0.95	0.3607	-0.159197	0.054977
Intercep	-34.05751	3.82881873	-8.90	<.0001	-41.561857	-26.553163

Weighted Sum of Squares = 10.273044977

Degrees of Freedom = 11

RLS Scale Estimate = 0.9663918355

Cov Matrix of Parameter Estimates
	VAR1	VAR2	VAR3	Intercep
VAR1	0.0061791648	-0.005776855	-0.002300587	-0.034290068
VAR2	-0.005776855	0.0185096933	0.0002582502	-0.069740883
VAR3	-0.002300587	0.0002582502	0.0029852254	-0.131487406
Intercep	-0.034290068	-0.069740883	-0.131487406	14.659852903

Weighted R-squared = 0.9622869127

F(3,11) Statistic = 93.558645037

Probability = 4.1136826E-8

There are 15 points with nonzero weight.

Average Weight = 0.7142857143

The run has been executed successfully.

The preceding program produces the following output associated with the LTS analysis. In this analysis, observations, 1, 2, 3, 4, 13, and 21 have scaled residuals larger than 2.5 (table not shown) and are considered outliers.

See the documentation for the LMS subroutine for additional details.