Elementwise binary operators produce a result matrix from element-by-element operations on two argument matrices.

Table 5.2 lists the elementwise binary operators.

For example, consider the following two matrices:

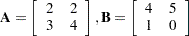The addition operator adds corresponding matrix elements, as follows:

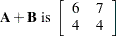The elementwise multiplication operator multiplies corresponding elements, as follows:

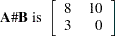The elementwise power operator 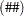raises elements to powers, as follows:

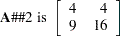The element maximum operator compares corresponding elements and chooses the larger, as follows:

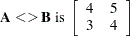The less than or equal to operator 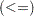returns a 1 if an element of 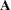is less than or equal to the corresponding element of 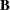, and returns a 0 otherwise:

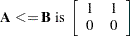All operators can work on scalars, vectors, or matrices, provided that the operation makes sense. For example, you can add a scalar to a matrix or divide a matrix by a scalar. For example, the following statement replaces each negative element of the matrix x with 0:

y = x#(x>0);

The expression x>0 is an operation that compares each element of x to (scalar) zero and creates a temporary matrix of results; an element of the temporary matrix is 1 when the corresponding element of x is positive, and 0 otherwise. The original matrix x is then multiplied elementwise by the temporary matrix, resulting in the matrix y. To fully understand the intermediate calculations, you can use the RESET statement with the PRINTALL option to have the temporary result matrices displayed.
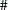
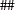
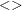
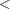
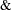
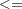
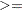