Iterative Methods
The conjugate gradient algorithm can be interpreted as the following optimization problem: minimize 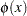 defined by
defined by
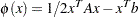 |
where 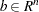 and
and 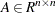 are symmetric and positive definite.
are symmetric and positive definite.
At each iteration 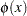 is minimized along an
is minimized along an 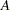 -conjugate direction, constructing orthogonal residuals:
-conjugate direction, constructing orthogonal residuals:
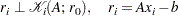 |
where 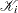 is a Krylov subspace:
is a Krylov subspace:
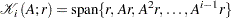 |
Minimum residual algorithms work by minimizing the Euclidean norm 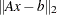 over
over 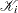 . At each iteration,
. At each iteration, 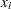 is the vector in
is the vector in 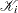 that gives the smallest residual.
that gives the smallest residual.
The biconjugate gradient algorithm belongs to a more general class of Petrov-Galerkin methods, where orthogonality is enforced in a different 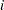 -dimensional subspace (
-dimensional subspace (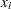 remains in
remains in 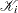 ):
):
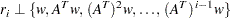 |