Consider the following small exampl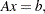e: where

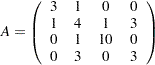and the vector of right-hand sides 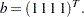Since the matrix is positive definite and symmetric, you can apply the conjugate gradient algorithm to solve the system. Remember that you must specify only the lower-triangular part of the matrix (so row indices must be greater than or equal to the corresponding column indices.)

The code for this example is as follows:

   /* value   row   col */
   A = { 3     1     1,
         1     2     1,
         4     2     2,
         1     3     2,
         3     4     2,
        10     3     3,
         3     4     4 };

   /* right-hand sides */
   b = {1, 1, 1, 1};

   /* desired solution tolerance (optional) */
   tol = 1e-7;

   /* maximum number of iterations (optional) */
   maxit = 200;

   /* allocate iteration progress (optional) */
   hist = j(50, 1);

   /* provide an initial guess (optional) */
   start = {2, 3, 4, 5};

   /* invoke conjugate gradient method */
   call itsolver (
      x, st, it,          /* output parameters */
      'cg', A, b, 'ic',   /* input parameters */
      tol,                /* optional control parameters */
      maxit,
      start,
      hist
    );

   print  x;  /* print solution */
   print st;  /* print solution tolerance */
   print it;  /* print resultant number of iterations */

Notice that the example used an incomplete Cholesky preconditioner (which is recommended). Here is the program output:

                    X
                0.5882353
                -0.764706
                0.1764706
                1.0980392

                    ST
                1.961E-16

                    IT
                        3

The conjugate gradient method converged successfully within three iterations. You can also print out the hist (iteration progress) array. Different starting points result in different iterative histories.