| SVD Call |
The SVD subroutine computes the singular value decomposition for a numerical matrix. The input to the SVD subroutine is as follows:
- a
-
is the
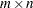 input matrix that is factored as described in the following discussion.
input matrix that is factored as described in the following discussion. The SVD subroutine returns the following output arguments:
- u
is an
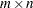 orthonormal matrix
orthonormal matrix - q
is an
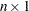 vector that contains the singular values
vector that contains the singular values - v
is an
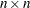 orthonormal matrix
orthonormal matrix
If 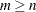 , the SVD subroutine factors a real
, the SVD subroutine factors a real 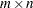 matrix
matrix  into the form
into the form
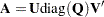 |
where
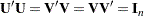 |
and 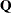 contains the singular values of
contains the singular values of 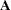 . The columns of
. The columns of 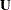 contains of the orthonormal eigenvectors of
contains of the orthonormal eigenvectors of 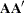 , and
, and 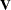 contains the orthonormal eigenvectors of
contains the orthonormal eigenvectors of 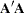 .
. 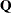 contains the square roots of the eigenvalues of
contains the square roots of the eigenvalues of 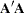 and
and 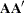 , except for some zeros.
, except for some zeros.
If 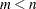 , a corresponding decomposition is done where
, a corresponding decomposition is done where 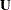 and
and 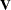 switch roles:
switch roles:
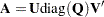 |
where
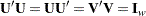 |
The singular values are sorted in descending order.
For information about the method used in the SVD subroutine, see Wilkinson and Reinsch (1971).
The following example is taken from Wilkinson and Reinsch (1971):
a = {22 10 2 3 7,
14 7 10 0 8,
-1 13 -1 -11 3,
-3 -2 13 -2 4,
9 8 1 -2 4,
9 1 -7 5 -1,
2 -6 6 5 1,
4 5 0 -2 2};
call svd(u, q, v, a);
print u, q, v;
/* check correctness of factors */
zero = ssq(a - u*diag(q)*v`);
reset fuzz; /* print small numbers as zero */
print zero;
The matrix is rank-3 with exact singular values 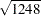 ,
, 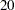 ,
, 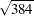 ,
, 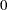 , and
, and 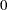 . Because of the repeated singular values, the last two columns of the
. Because of the repeated singular values, the last two columns of the 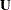 matrix are not uniquely determined. A valid result is shown in Figure 23.285:
matrix are not uniquely determined. A valid result is shown in Figure 23.285:
| u | ||||
|---|---|---|---|---|
| 0.7071068 | 0.1581139 | -0.176777 | -0.328209 | -0.328056 |
| 0.5303301 | 0.1581139 | 0.3535534 | 0.5309976 | 0.0489362 |
| 0.1767767 | -0.790569 | 0.1767767 | -0.413567 | 0.1307398 |
| 0 | 0.1581139 | 0.7071068 | -0.266418 | 0.0321656 |
| 0.3535534 | -0.158114 | 0 | 0.0253566 | -0.041441 |
| 0.1767767 | 0.1581139 | -0.53033 | -0.19666 | 0.3666144 |
| 0 | 0.4743416 | 0.1767767 | -0.500944 | 0.4145131 |
| 0.1767767 | -0.158114 | 0 | 0.2793571 | 0.7509412 |
| q |
|---|
| 35.327043 |
| 20 |
| 19.595918 |
| 1.1E-15 |
| 5.501E-16 |
| v | ||||
|---|---|---|---|---|
| 0.8006408 | 0.3162278 | -0.288675 | -0.419095 | 0 |
| 0.4803845 | -0.632456 | 0 | 0.4405091 | 0.4185481 |
| 0.1601282 | 0.3162278 | 0.8660254 | -0.052005 | 0.3487901 |
| 0 | 0.6324555 | -0.288675 | 0.6760591 | 0.244153 |
| 0.3202563 | 0 | 0.2886751 | 0.4129773 | -0.802217 |
| zero |
|---|
| 0 |
The SVD routine performs most of its computations in the memory allocated for returning the singular value decomposition.