HANKEL(
matrix )
;
The HANKEL function generates a Hankel matrix from a vector or a block Hankel matrix from a matrix. A block Hankel matrix has the property that all matrices on the reverse diagonals are the same. The argument matrix is an 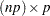 or
or 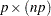 matrix; the value returned is the
matrix; the value returned is the 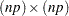 result.
result.
The Hankel function uses the first  submatrix
submatrix  of the argument matrix as the blocks of the first reverse diagonal. The second
of the argument matrix as the blocks of the first reverse diagonal. The second  submatrix
submatrix 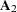 of the argument matrix forms the second reverse diagonal. The remaining reverse diagonals are formed accordingly. After the values in the argument matrix have all been placed, the rest of the matrix is filled in with 0. If
of the argument matrix forms the second reverse diagonal. The remaining reverse diagonals are formed accordingly. After the values in the argument matrix have all been placed, the rest of the matrix is filled in with 0. If 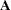 is
is 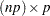 , then the first
, then the first 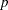 columns of the returned matrix,
columns of the returned matrix, 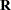 , are the same as
, are the same as 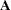 . If
. If 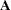 is
is 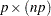 , then the first
, then the first 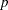 rows of
rows of 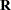 are the same as
are the same as 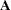 .
.
The HANKEL function is especially useful in time series applications that involve a set of variables that represent the present and past and a set of variables that represent the present and future. In this situation, the covariance matrix between the sets of variables is often assumed to be a block Hankel matrix. If
and if 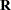 is the matrix formed by the HANKEL function, then
is the matrix formed by the HANKEL function, then
If
and if 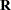 is the matrix formed by the HANKEL function, then
is the matrix formed by the HANKEL function, then
For example, the following statements produce Hankel matrices, as shown in Figure 23.130:
r1 = hankel({1 2 3 4 5});
r2 = hankel({1 2 ,
3 4 ,
5 6 ,
7 8});
r3 = hankel({1 2 3 4 ,
5 6 7 8});
print r1, r2, r3;
Figure 23.130
Hankel Matrices
| 1 |
2 |
3 |
4 |
5 |
| 2 |
3 |
4 |
5 |
0 |
| 3 |
4 |
5 |
0 |
0 |
| 4 |
5 |
0 |
0 |
0 |
| 5 |
0 |
0 |
0 |
0 |
| 1 |
2 |
5 |
6 |
| 3 |
4 |
7 |
8 |
| 5 |
6 |
0 |
0 |
| 7 |
8 |
0 |
0 |
| 1 |
2 |
3 |
4 |
| 5 |
6 |
7 |
8 |
| 3 |
4 |
0 |
0 |
| 7 |
8 |
0 |
0 |
Copyright © SAS Institute Inc. All rights reserved.
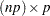 or
or 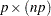 matrix; the value returned is the
matrix; the value returned is the 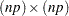 result.
result.  submatrix
submatrix  of the argument matrix as the blocks of the first reverse diagonal. The second
of the argument matrix as the blocks of the first reverse diagonal. The second  submatrix
submatrix 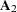 of the argument matrix forms the second reverse diagonal. The remaining reverse diagonals are formed accordingly. After the values in the argument matrix have all been placed, the rest of the matrix is filled in with 0. If
of the argument matrix forms the second reverse diagonal. The remaining reverse diagonals are formed accordingly. After the values in the argument matrix have all been placed, the rest of the matrix is filled in with 0. If 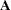 is
is 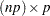 , then the first
, then the first 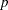 columns of the returned matrix,
columns of the returned matrix, 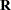 , are the same as
, are the same as 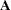 . If
. If 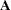 is
is 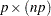 , then the first
, then the first 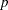 rows of
rows of 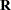 are the same as
are the same as 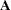 .
. 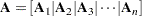
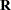 is the matrix formed by the HANKEL function, then
is the matrix formed by the HANKEL function, then 
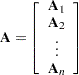
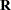 is the matrix formed by the HANKEL function, then
is the matrix formed by the HANKEL function, then 