| Multiplication Operator, Elementwise: # |
- matrix1 # matrix2 ;
- matrix # scalar ;
- matrix # vector ;
The elementwise multiplication operator (#) computes a new matrix with elements that are the products of the corresponding elements of matrix1 and matrix2.
For example, the following statements compute the matrix ab, shown in Figure 23.17:
a = {1 2,
3 4};
b = {4 8,
0 5};
ab = a#b;
print ab;
| ab | |
|---|---|
| 4 | 16 |
| 0 | 20 |
In addition to multiplying matrices that have the same dimensions, you can use the elementwise multiplication operator to multiply a matrix and a scalar.
When either argument is a scalar, each element in matrix is multiplied by the scalar value.
-
When you use the matrix # vector form, each row or column of the
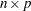 matrix is multiplied by a corresponding element of the vector.
matrix is multiplied by a corresponding element of the vector. If you multiply by an
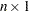 column vector, each row of the matrix is multiplied by the corresponding row of the vector.
column vector, each row of the matrix is multiplied by the corresponding row of the vector. If you multiply by a
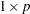 row vector, each column of the matrix is multiplied by the corresponding column of the vector.
row vector, each column of the matrix is multiplied by the corresponding column of the vector.
For example, a 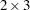 matrix can be multiplied on either side by a
matrix can be multiplied on either side by a 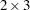 ,
, 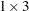 ,
, 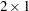 , or
, or  matrix. The following statements multiply the
matrix. The following statements multiply the 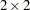 matrix a by a column vector and a row vector. The results are shown in Figure 23.18.
matrix a by a column vector and a row vector. The results are shown in Figure 23.18.
c = {10, 100}; /* column vector */
r = {10 100}; /* row vector */
ac = a#c;
ar = a#r;
print ac, ar;
| ac | |
|---|---|
| 10 | 20 |
| 300 | 400 |
| ar | |
|---|---|
| 10 | 200 |
| 30 | 400 |
Elementwise multiplication is also known as the Schur or Hadamard product. Elementwise multiplication (which uses the # operator) should not be confused with matrix multiplication (which uses the * operator).
When an element of a matrix contains a missing value, the corresponding element of the product is also a missing value.