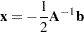A regression model with a complete quadratic set of regressions across several factors can be processed to yield the estimated critical values that can optimize a response. First, the regression is performed for two variables according to the model
The estimates are then divided into a vector of linear coefficients (estimates) 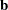 and a matrix of quadratic coefficients
and a matrix of quadratic coefficients 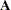 . The solution for critical values is
. The solution for critical values is
The following program creates a module to perform quadratic response surface regression.
/* Quadratic Response Surface Regression */
/* This matrix routine reads in the factor variables and */
/* the response, forms the quadratic regression model and */
/* estimates the parameters, and then solves for the optimal */
/* response, prints the optimal factors and response, and */
/* displays the eigenvalues and eigenvectors of the */
/* matrix of quadratic parameter estimates to determine if */
/* the solution is a maximum or minimum, or saddlepoint, and */
/* which direction has the steepest and gentlest slopes. */
/* */
/* Given that d contains the factor variables, */
/* and y contains the response. */
/* */
start rsm;
n=nrow(d);
k=ncol(d); /* dimensions */
x=j(n,1,1)||d; /* set up design matrix */
do i=1 to k;
do j=1 to i;
x=x||d[,i] #d[,j];
end;
end;
beta=solve(x`*x,x`*y); /* solve parameter estimates */
print "Parameter Estimates" , beta;
c=beta[1]; /* intercept estimate */
b=beta[2:(k+1)]; /* linear estimates */
a=j(k,k,0);
L=k+1; /* form quadratics into matrix */
do i=1 to k;
do j=1 to i;
L=L+1;
a[i,j]=beta [L,];
end;
end;
a=(a+a`)*.5; /* symmetrize */
xx=-.5*solve(a,b); /* solve for critical value */
print , "Critical Factor Values" , xx;
/* Compute response at critical value */
yopt=c + b`*xx + xx`*a*xx;
print , "Response at Critical Value" yopt;
call eigen(eval,evec,a);
print , "Eigenvalues and Eigenvectors", eval, evec;
if min(eval)>0 then print , "Solution Was a Minimum";
if max(eval)<0 then print , "Solution Was a Maximum";
finish rsm;
/* Sample Problem with Two Factors */
d={-1 -1, -1 0, -1 1,
0 -1, 0 0, 0 1,
1 -1, 1 0, 1 1};
y={ 71.7, 75.2, 76.3, 79.2, 81.5, 80.2, 80.1, 79.1, 75.8};
run rsm;
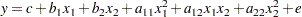
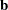 and a matrix of quadratic coefficients
and a matrix of quadratic coefficients 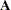 . The solution for critical values is
. The solution for critical values is