Example 9.2 Newton’s Method for Solving Nonlinear Systems of Equations
This example solves a nonlinear system of equations by Newton’s method. Let the nonlinear system be represented by
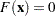 |
where  is a vector and
is a vector and 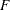 is a vector-valued, possibly nonlinear function.
is a vector-valued, possibly nonlinear function.
In order to find  such that
such that 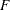 goes to 0, an initial estimate
goes to 0, an initial estimate 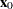 is chosen, and Newton’s iterative method for converging to the solution is used:
is chosen, and Newton’s iterative method for converging to the solution is used:
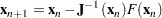 |
where  is the Jacobian matrix of partial derivatives of
is the Jacobian matrix of partial derivatives of 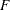 with respect to
with respect to  . (For more efficient computations, use the built-in NLPNRA subroutine.)
. (For more efficient computations, use the built-in NLPNRA subroutine.)
For optimization problems, the same method is used, where 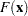 is the gradient of the objective function and
is the gradient of the objective function and  becomes the Hessian (Newton-Raphson).
becomes the Hessian (Newton-Raphson).
In this example, the system to be solved is
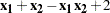 |
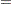 |
 |
|||
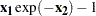 |
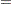 |
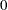 |
The following statements are organized into three modules: NEWTON, FUN, and DERIV.
/* Newton's Method to Solve a Nonlinear Function */
/* The user must supply initial values, */
/* and the FUN and DERIV functions. */
/* On entry: FUN evaluates the function f in terms of x */
/* initial values are given to x */
/* DERIV evaluates jacobian j */
/* tuning variables: CONVERGE, MAXITER. */
/* On exit: solution in x, function value in f close to 0 */
/* ITER has number of iterations. */
proc iml;
start newton;
run fun; /* evaluate function at starting values */
do iter = 1 to maxiter /* iterate until maxiter */
while(max(abs(f))>converge); /* iterations or convergence */
run deriv; /* evaluate derivatives in j */
delta = -solve(j,f); /* solve for correction vector */
x = x+delta; /* the new approximation */
run fun; /* evaluate the function */
end;
finish newton;
maxiter = 15; /* default maximum iterations */
converge = .000001; /* default convergence criterion */
/* User-supplied function evaluation */
start fun;
x1 = x[1] ;
x2 = x[2] ; /* extract the values */
f = (x1+x2-x1*x2+2) //
(x1*exp(-x2)-1); /* evaluate the function */
finish fun;
/* User-supplied derivatives of the function */
start deriv;
/* evaluate jacobian */
j = ((1-x2)||(1-x1) ) // (exp(-x2)||(-x1*exp(-x2)));
finish deriv;
do;
print "Solving the system: X1+X2-X1*X2+2=0, X1*EXP(-X2)-1=0" ,;
x={.1, -2}; /* starting values */
run newton;
print x f;
end;
The results are shown in Output 9.2.1.
| Solving the system: X1+X2-X1*X2+2=0, X1*EXP(-X2)-1=0 |
| x | f |
|---|---|
| 0.0977731 | 5.3523E-9 |
| -2.325106 | 6.1501E-8 |