Tutorial: A Module for Linear Regression: Low-Resolution Plots

Tutorial: A Module for Linear Regression

Low-Resolution Plots

You can continue the example of this chapter by using the PGRAF subroutine to create a low-resolution plots.

The following statements plot the residual values versus the explanatory variable:

xy = x1 || resid;
reset linesize=78 pagesize=20;
call pgraf(xy,'r','x','Residuals','Plot of Residuals');

The first statement creates a matrix by using the horizontal concatenation operator (||) to concatenate x1 with resid. The two-column matrix xy contains the pairs of points that the PGRAF subroutine plots. The PGRAF call produces the desired plot, as shown in Figure 4.8.

Figure 4.8 Residual Plot from the PGRAF Subroutine

                             Plot of Residuals                                
     |                                                                        
   2 +                                                                        
R    |                                                                        
e    |                                                 r                      
s    |                     r                                                  
i    |                                                                        
d    |                                                                        
u  0 +                                                                        
a    |       r                                                       r        
l    |                                                                        
s    |                                                                        
     |                                                                        
     |                                   r                                    
  -2 +                                                                        
     --------+------+------+------+------+------+------+------+------+--------
            1.0    1.5    2.0    2.5    3.0    3.5    4.0    4.5    5.0       
                                                                              
                                         x

The arguments to PGRAF are as follows:

an 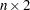$\text{[math]}$ matrix that contains the pairs of points
a plotting symbol
a label for the X axis
a label for the Y axis
a title for the plot

You can also plot the predicted values 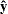$\text{[math]}$ against $\text{[math]}$ . You can create a matrix (say, xyh) that contains the points to plot by concatenating x1 with yhat. The PGRAF subroutine plots the points, as shown in the following statements. The resulting plot is shown in Figure 4.9.

xyh = x1 || yhat;
call pgraf(xyh,'*','x','Predicted','Plot of Predicted Values');

Figure 4.9 Predicted Value Plot from the PGRAF Subroutine

                          Plot of Predicted Values                            
     |                                                                        
  40 +                                                                        
P    |                                                               *        
r    |                                                                        
e    |                                                                        
d    |                                                                        
i    |                                                                        
c 20 +                                                 *                      
t    |                                                                        
e    |                                                                        
d    |                                   *                                    
     |                                                                        
     |                     *                                                  
   0 +       *                                                                
     --------+------+------+------+------+------+------+------+------+--------
            1.0    1.5    2.0    2.5    3.0    3.5    4.0    4.5    5.0       
                                                                              
                                         x

You can also use the PGRAF subroutine to create a low-resolution plot of the predicted and observed values plotted against the explanatory variable, as shown in the following statements:

n = nrow(x1);                        /* number of observations */
newxy = (x1//x1) || (y//yhat);       /* observed followed by predicted */
label = repeat('y',n,1) // repeat('p',n,1);/* 'y' followed by 'p' */
call pgraf(newxy,label,'x','y','Scatter Plot with Regression Line' );

The NROW function returns the number of rows of x1. The example creates a matrix newxy, which contains the pairs of all observed values, followed by the pairs of predicted values. (Notice that you need to use both the horizontal concatenation operator (||) and the vertical concatenation operator (//).) The matrix label contains the character label for each point: a "y" for each observed point and a "p" for each predicted point. Finally, the PGRAF subroutine plots the observed and predicted values by using the corresponding symbols, as shown in Figure 4.9.

For several points in Figure 4.8, the observed and predicted values are too close together to be distinguishable in the low-resolution plot.

Figure 4.10 Plot of Predicted and Observed Values

                     Scatter Plot with Regression Line                        
     |                                                                        
  40 +                                                                        
     |                                                               y        
     |                                                                        
     |                                                                        
     |                                                                        
y    |                                                 y                      
  20 +                                                 p                      
     |                                                                        
     |                                                                        
     |                                   y                                    
     |                     y                                                  
     |                     p                                                  
   0 +       y                                                                
     --------+------+------+------+------+------+------+------+------+--------
            1.0    1.5    2.0    2.5    3.0    3.5    4.0    4.5    5.0       
                                                                              
                                         x

Top of Page