| Time Series Analysis and Examples |
| Getting Started |
The fractional differencing enables the degree of differencing 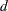 to take any real value rather than being restricted to integer values. The fractionally differenced processes are capable of modeling long-term persistence. The process
to take any real value rather than being restricted to integer values. The fractionally differenced processes are capable of modeling long-term persistence. The process
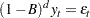 |
is known as a fractional Gaussian noise process or an ARFIMA(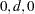 ) process, where
) process, where 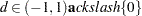 ,
, 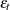 is a white noise process with mean zero and variance
is a white noise process with mean zero and variance 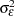 , and
, and 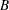 is the backshift operator such that
is the backshift operator such that 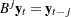 . The extension of an ARFIMA(
. The extension of an ARFIMA(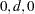 ) model combines fractional differencing with an ARMA(
) model combines fractional differencing with an ARMA(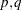 ) model, known as an ARFIMA(
) model, known as an ARFIMA(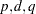 ) model.
) model.
Consider an ARFIMA(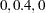 ) represented as
) represented as 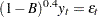 where
where 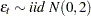 . With the following statements you can
. With the following statements you can
generate the simulated 300 observations data
obtain the fractionally differenced data
compute the autocovariance function
compute the log-likelihood function
fit a fractionally integrated time series model to the data
proc iml; /* ARFIMA(0,0.4,0) */ lag = (0:12)`; call farmacov(autocov_D_IS_04, 0.4); call farmacov(D_IS_005, 0.05); print lag autocov_D_IS_04 D_IS_005; d = 0.4; call farmasim(yt, d) n = 300 sigma = 2 seed=5345; print yt; call fdif(zt, yt, d); print zt; call farmalik(lnl, yt, d); print lnl; call farmafit(d, ar, ma, sigma, yt); print d sigma;
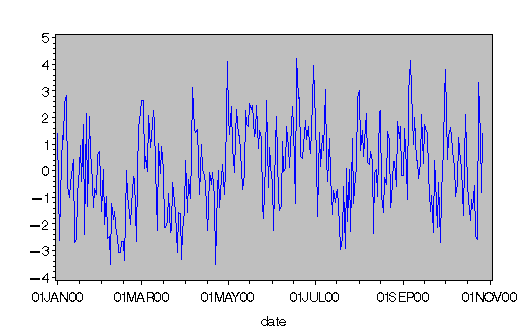
The FARMASIM function generates the data shown in Figure 13.4.9.
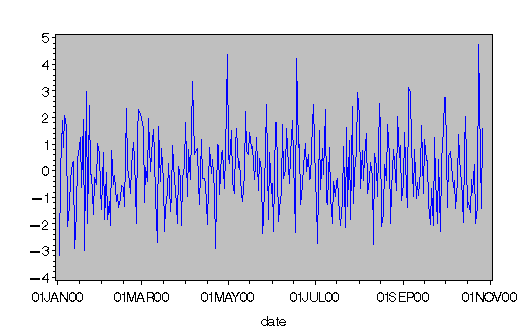
The FDIF function creates the fractionally differenced process. Figure 13.4.10 shows a white noise series.
| Diffuse Kalman Filtering |
| lag | autocov_D_IS_04 | D_IS_005 |
|---|---|---|
| 0 | 2.0700983 | 1.0044485 |
| 1 | 1.3800656 | 0.0528657 |
| 2 | 1.2075574 | 0.0284662 |
| 3 | 1.1146683 | 0.0197816 |
| 4 | 1.0527423 | 0.0152744 |
| 5 | 1.0069709 | 0.0124972 |
| 6 | 0.9710077 | 0.0106069 |
| 7 | 0.9415832 | 0.0092333 |
| 8 | 0.9168047 | 0.008188 |
| 9 | 0.8954836 | 0.0073647 |
| 10 | 0.8768277 | 0.0066985 |
| 11 | 0.8602838 | 0.006148 |
| 12 | 0.8454513 | 0.0056849 |
The first column is the autocovariance function of the ARFIMA(0,0.4,0) model, and the second column is the autocovariance function of the ARFIMA(0,0.05,0) model. The first column decays to zero more slowly than the second column.
The first row value is the log-likelihood function of the ARFIMA(0,0.4,0) model. Since the default option of the estimates method is the conditional sum of squares, the last two rows of Figure 13.4.12 do not have the values since the default estimation method is used.
The final estimates of the parameters are 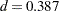 and
and 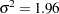 , while the true values of the data generating process are
, while the true values of the data generating process are 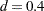 and
and 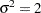 .
.
Copyright © SAS Institute, Inc. All Rights Reserved.