Robust Regression Examples :: SAS/IML(R) 9.22 User's Guide

Robust Regression Examples

Example 12.6 Hawkins-Bradu-Kass Data

The first 14 observations of the following data set (see Hawkins, Bradu, and Kass (1984)) are leverage points; however, only observations 12, 13, and 14 have large 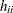$\text{[math]}$ , and only observations 12 and 14 have large $\text{[math]}$ values.

title "Hawkins, Bradu, Kass (1984) Data";
aa = { 1  10.1  19.6  28.3   9.7,
       2   9.5  20.5  28.9  10.1,
       3  10.7  20.2  31.0  10.3,
       4   9.9  21.5  31.7   9.5,
       5  10.3  21.1  31.1  10.0,
       6  10.8  20.4  29.2  10.0,
       7  10.5  20.9  29.1  10.8,
       8   9.9  19.6  28.8  10.3,
       9   9.7  20.7  31.0   9.6,
      10   9.3  19.7  30.3   9.9,
      11  11.0  24.0  35.0  -0.2,
      12  12.0  23.0  37.0  -0.4,
      13  12.0  26.0  34.0   0.7,
      14  11.0  34.0  34.0   0.1,
      15   3.4   2.9   2.1  -0.4,
      16   3.1   2.2   0.3   0.6,
      17   0.0   1.6   0.2  -0.2,
      18   2.3   1.6   2.0   0.0,
      19   0.8   2.9   1.6   0.1,
      20   3.1   3.4   2.2   0.4,
      21   2.6   2.2   1.9   0.9,
      22   0.4   3.2   1.9   0.3,
      23   2.0   2.3   0.8  -0.8,
      24   1.3   2.3   0.5   0.7,
      25   1.0   0.0   0.4  -0.3,
      26   0.9   3.3   2.5  -0.8,
      27   3.3   2.5   2.9  -0.7,
      28   1.8   0.8   2.0   0.3,
      29   1.2   0.9   0.8   0.3,
      30   1.2   0.7   3.4  -0.3,
      31   3.1   1.4   1.0   0.0,
      32   0.5   2.4   0.3  -0.4,
      33   1.5   3.1   1.5  -0.6,
      34   0.4   0.0   0.7  -0.7,
      35   3.1   2.4   3.0   0.3,
      36   1.1   2.2   2.7  -1.0,
      37   0.1   3.0   2.6  -0.6,
      38   1.5   1.2   0.2   0.9,
      39   2.1   0.0   1.2  -0.7,
      40   0.5   2.0   1.2  -0.5,
      41   3.4   1.6   2.9  -0.1,
      42   0.3   1.0   2.7  -0.7,
      43   0.1   3.3   0.9   0.6,
      44   1.8   0.5   3.2  -0.7,
      45   1.9   0.1   0.6  -0.5,
      46   1.8   0.5   3.0  -0.4,
      47   3.0   0.1   0.8  -0.9,
      48   3.1   1.6   3.0   0.1,
      49   3.1   2.5   1.9   0.9,
      50   2.1   2.8   2.9  -0.4,
      51   2.3   1.5   0.4   0.7,
      52   3.3   0.6   1.2  -0.5,
      53   0.3   0.4   3.3   0.7,
      54   1.1   3.0   0.3   0.7,
      55   0.5   2.4   0.9   0.0,
      56   1.8   3.2   0.9   0.1,
      57   1.8   0.7   0.7   0.7,
      58   2.4   3.4   1.5  -0.1,
      59   1.6   2.1   3.0  -0.3,
      60   0.3   1.5   3.3  -0.9,
      61   0.4   3.4   3.0  -0.3,
      62   0.9   0.1   0.3   0.6,
      63   1.1   2.7   0.2  -0.3,
      64   2.8   3.0   2.9  -0.5,
      65   2.0   0.7   2.7   0.6,
      66   0.2   1.8   0.8  -0.9,
      67   1.6   2.0   1.2  -0.7,
      68   0.1   0.0   1.1   0.6,
      69   2.0   0.6   0.3   0.2,
      70   1.0   2.2   2.9   0.7,
      71   2.2   2.5   2.3   0.2,
      72   0.6   2.0   1.5  -0.2,
      73   0.3   1.7   2.2   0.4,
      74   0.0   2.2   1.6  -0.9,
      75   0.3   0.4   2.6   0.2 };

a = aa[,2:4]; b = aa[,5];

The data are also listed in Rousseeuw and Leroy (1987).

The complete enumeration must inspect 1,215,450 subsets.

Output 12.6.1 displays the iteration history for MVE.

optn = j(9,1,.);
optn[1]= 3;              /* ipri */
optn[2]= 1;              /* pcov: print COV */
optn[3]= 1;              /* pcor: print CORR */
optn[5]= -1;             /* nrep: all subsets */
    
call mve(sc,xmve,dist,optn,a);

Output 12.6.1 Iteration History for MVE

Hawkins, Bradu, Kass (1984) Data

Subset	Singular	Best Criterion	Percent
121545	0	51.104276	10
243090	1	51.104276	20
364635	1	51.104276	30
486180	2	51.104276	40
607725	3	51.104276	50
729270	9	6.271725	60
850815	35	6.271725	70
972360	55	5.912308	80
1093905	76	5.912308	90
1215450	114	5.912308	100

Output 12.6.2 reports the robust parameter estimates for MVE.

Output 12.6.2 Robust Location Estimates

Robust MVE Location Estimates
VAR1	1.5133333333
VAR2	1.8083333333
VAR3	1.7016666667

Robust MVE Scatter Matrix
	VAR1	VAR2	VAR3
VAR1	1.1143954802	0.0939548023	0.1416723164
VAR2	0.0939548023	1.1231497175	0.1174435028
VAR3	0.1416723164	0.1174435028	1.0747429379

Output 12.6.3 reports the eigenvalues of the robust scatter matrix and the robust correlation matrix.

Output 12.6.3 MVE Scatter Matrix

Eigenvalues of Robust Scatter Matrix
VAR1	1.3396371545
VAR2	1.0281247572
VAR3	0.9445262239

Robust Correlation Matrix
	VAR1	VAR2	VAR3
VAR1	1	0.0839808925	0.1294532696
VAR2	0.0839808925	1	0.1068951177
VAR3	0.1294532696	0.1068951177	1

Output 12.6.4 shows the classical Mahalanobis and robust distances obtained by complete enumeration. The first 14 observations are recognized as outliers (leverage points).

Output 12.6.4 Mahalanobis and Robust Distances

Classical Distances and Robust (Rousseeuw) Distances
Unsquared Mahalanobis Distance and
Unsquared Rousseeuw Distance of Each Observation
N	Mahalanobis Distances	Robust Distances	Weight
1	1.916821	29.541649	0
2	1.855757	30.344481	0
3	2.313658	31.985694	0
4	2.229655	33.011768	0
5	2.100114	32.404938	0
6	2.146169	30.683153	0
7	2.010511	30.794838	0
8	1.919277	29.905756	0
9	2.221249	32.092048	0
10	2.333543	31.072200	0
11	2.446542	36.808021	0
12	3.108335	38.071382	0
13	2.662380	37.094539	0
14	6.381624	41.472255	0
15	1.815487	1.994672	1.000000
16	2.151357	2.202278	1.000000
17	1.384915	1.918208	1.000000
18	0.848155	0.819163	1.000000
19	1.148941	1.288387	1.000000
20	1.591431	2.046703	1.000000
21	1.089981	1.068327	1.000000
22	1.548776	1.768905	1.000000
23	1.085421	1.166951	1.000000
24	0.971195	1.304648	1.000000
25	0.799268	2.030417	1.000000
26	1.168373	1.727131	1.000000
27	1.449625	1.983831	1.000000
28	0.867789	1.073856	1.000000
29	0.576399	1.168060	1.000000
30	1.568868	2.091386	1.000000
31	1.838496	1.793386	1.000000
32	1.307230	1.743558	1.000000
33	0.981988	1.264121	1.000000
34	1.175014	2.052641	1.000000
35	1.243636	1.872695	1.000000
36	0.850804	1.136658	1.000000
37	1.832378	2.050041	1.000000
38	0.752061	1.522734	1.000000
39	1.265041	1.885970	1.000000
40	1.112038	1.068841	1.000000
41	1.699757	2.063398	1.000000
42	1.765040	1.785637	1.000000
43	1.870090	2.166100	1.000000
44	1.420448	2.018610	1.000000
45	1.075973	1.944449	1.000000
46	1.344171	1.872483	1.000000
47	1.966328	2.408721	1.000000
48	1.424238	1.892539	1.000000
49	1.569756	1.594109	1.000000
50	0.423972	1.458595	1.000000
51	1.302651	1.569843	1.000000
52	2.076055	2.205601	1.000000
53	2.210443	2.492631	1.000000
54	1.414288	1.884937	1.000000
55	1.230455	1.360622	1.000000
56	1.331101	1.626276	1.000000
57	0.832744	1.432408	1.000000
58	1.404401	1.723091	1.000000
59	0.591235	1.263700	1.000000
60	1.889737	2.087849	1.000000
61	1.674945	2.286045	1.000000
62	0.759533	2.024702	1.000000
63	1.292259	1.783035	1.000000
64	0.973868	1.835207	1.000000
65	1.148208	1.562278	1.000000
66	1.296746	1.444491	1.000000
67	0.629827	0.552899	1.000000
68	1.549548	2.101580	1.000000
69	1.070511	1.827919	1.000000
70	0.997761	1.354151	1.000000
71	0.642927	0.988770	1.000000
72	1.053395	0.908316	1.000000
73	1.472178	1.314779	1.000000
74	1.646461	1.516083	1.000000
75	1.899178	2.042560	1.000000

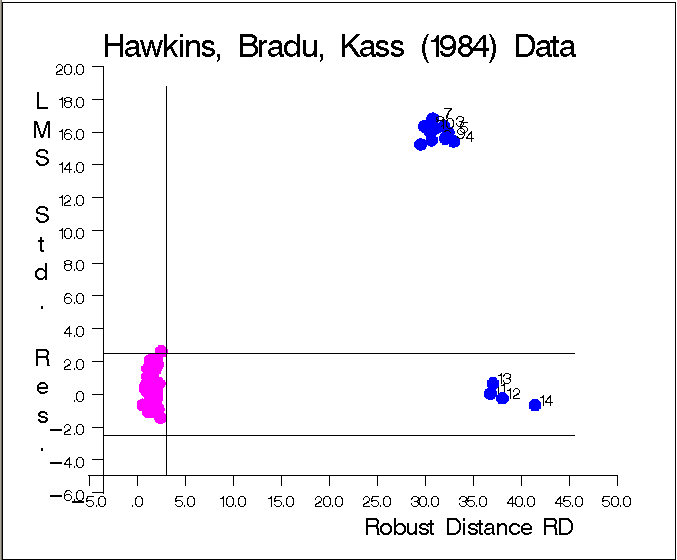
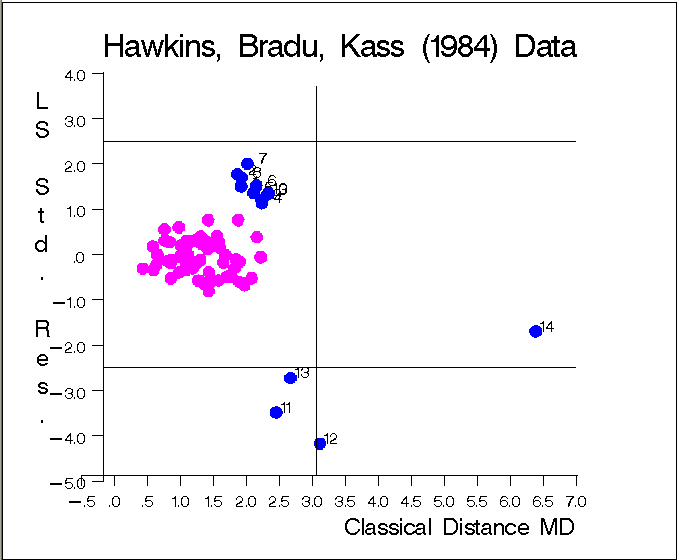
The graphs in Figure 12.6.5 and Figure 12.6.6 show the following:

the plot of standardized LMS residuals vs. robust distances $\text{[math]}$
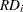
the plot of standardized LS residuals vs. Mahalanobis distances $\text{[math]}$

The graph identifies the four good leverage points 11, 12, 13, and 14, which have small standardized LMS residuals but large robust distances, and the 10 bad leverage points $\text{[math]}$ , which have large standardized LMS residuals and large robust distances.

Output 12.6.5 Hawkins-Bradu-Kass Data: LMS Residuals vs. Robust Distances

Output 12.6.6 Hawkins-Bradu-Kass Data: LS Residuals vs. Mahalanobis Distances

Top of Page