Example 12.1 LMS and LTS with Substantial Leverage Points: Hertzsprung-Russell Star Data

The following data are reported in Rousseeuw and Leroy (1987) and are based on Humphreys (1978) and Vansina and De Greve, J. P. (1982). The 47 observations correspond to the 47 stars of the CYG OB1 cluster in the direction of the constellation Cygnus. The regressor variable (column 2) is the logarithm of the effective temperature at the surface of the star (), and the response variable (column 3) 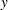is the logarithm of its light intensity (). The results for LS and LMS on page 28 of Rousseeuw and Leroy (1987) are based on a more precise (five decimal places) version of the data set. This data set is remarkable in that it contains four substantial leverage points (which represent giant stars) that greatly affect the results of and even regression. The high leverage points are observations 11, 20, 30, and 34.

ab =  { 1  4.37  5.23,   2  4.56  5.74,   3  4.26  4.93,
        4  4.56  5.74,   5  4.30  5.19,   6  4.46  5.46,
        7  3.84  4.65,   8  4.57  5.27,   9  4.26  5.57,
       10  4.37  5.12,  11  3.49  5.73,  12  4.43  5.45,
       13  4.48  5.42,  14  4.01  4.05,  15  4.29  4.26,
       16  4.42  4.58,  17  4.23  3.94,  18  4.42  4.18,
       19  4.23  4.18,  20  3.49  5.89,  21  4.29  4.38,
       22  4.29  4.22,  23  4.42  4.42,  24  4.49  4.85,
       25  4.38  5.02,  26  4.42  4.66,  27  4.29  4.66,
       28  4.38  4.90,  29  4.22  4.39,  30  3.48  6.05,
       31  4.38  4.42,  32  4.56  5.10,  33  4.45  5.22,
       34  3.49  6.29,  35  4.23  4.34,  36  4.62  5.62,
       37  4.53  5.10,  38  4.45  5.22,  39  4.53  5.18,
       40  4.43  5.57,  41  4.38  4.62,  42  4.45  5.06,
       43  4.50  5.34,  44  4.45  5.34,  45  4.55  5.54,
       46  4.45  4.98,  47  4.42  4.50 } ;

a = ab[,2]; b = ab[,3];

The following statements specify that most of the output be printed:

print "*** Hertzsprung-Russell Star Data: Do LMS ***";
optn = j(9,1,.);
optn[2]= 3;    /* ipri */
optn[3]= 3;    /* ilsq */
optn[8]= 3;    /* icov */

call lms(sc,coef,wgt,optn,b,a);

Some simple statistics for the independent and response variables are shown in Output 12.1.1.

Partial output for LS regression is shown in Output 12.1.2.

Output 12.1.3 displays the iteration history. Looking at the column Best Crit in the iteration history table, you see that, with complete enumeration, the optimal solution is quickly found.

The results of the optimization for LMS estimation are displayed in Output 12.1.4.

Output 12.1.5 displays the results for WLS regression. Due to the size of the scaled residuals, six observations (with numbers 7, 9, 11, 20, 30, 34) were assigned zero weights in the following WLS analysis.

The LTS regression implements the FAST-LTS algorithm, which improves the algorithm (used in SAS/IML Version 7 and earlier versions, denoted as V7 LTS in this chapter) in Rousseeuw and Leroy (1987) by using techniques called "selective iteration" and "nested extensions." These techniques are used in the C-steps of the algorithm. See Rousseeuw and Van Driessen (2000) for details. The FAST-LTS algorithm significantly improves the speed of computation.

The following statements implement the LTS regression on the Hertzsprung-Russell star data:

print "*** Hertzsprung-Russell Star Data: Do LTS ***";
optn = j(9,1,.);
optn[2]= 3;    /* ipri */
optn[3]= 3;    /* ilsq */
optn[8]= 3;    /* icov */

call lts(sc,coef,wgt,optn,b,a);

Output 12.1.6 summarizes the information for the LTS optimization.

Output 12.1.7 displays the optimization results and Output 12.1.8 displays the weighted LS regression based on LTS estimates.