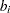| Nonlinear Optimization Examples |
Example 14.1 Chemical Equilibrium
The following example is used in many test libraries for nonlinear programming. It appeared originally in Bracken and McCormick (1968).
The problem is to determine the composition of a mixture of various chemicals that satisfy the mixture’s chemical equilibrium state. The second law of thermodynamics implies that at a constant temperature and pressure, a mixture of chemicals satisfies its chemical equilibrium state when the free energy of the mixture is reduced to a minimum. Therefore, the composition of the chemicals satisfying its chemical equilibrium state can be found by minimizing the free energy of the mixture.
The following notation is used in this problem:
|
number of chemical elements in the mixture |
|
number of compounds in the mixture |
|
number of moles for compound |
|
total number of moles in the mixture, |
|
number of atoms of element |
|
atomic weight of element |
The constraints for the mixture are as follows. Each of the compounds must have a nonnegative number of moles.
 |
There is a mass balance relationship for each element. Each relation is given by a linear equality constraint.
 |
The objective function is the total free energy of the mixture.
 |
where
 |
and  is the model standard free energy function for the
is the model standard free energy function for the  th compound. The value of
th compound. The value of  is found in existing tables.
is found in existing tables.  is the total pressure in atmospheres.
is the total pressure in atmospheres.
The problem is to determine the parameters  that minimize the objective function
that minimize the objective function 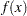 subject to the nonnegativity and linear balance constraints. To illustrate this, consider the following situation. Determine the equilibrium composition of compound
subject to the nonnegativity and linear balance constraints. To illustrate this, consider the following situation. Determine the equilibrium composition of compound  at temperature
at temperature  and pressure
and pressure  . The following table gives a summary of the information necessary to solve the problem.
. The following table gives a summary of the information necessary to solve the problem.
|
||||||
|
|
|
||||
|
Compound |
|
|
H |
N |
O |
1 |
|
|
|
1 |
||
2 |
|
|
|
2 |
||
3 |
|
|
|
2 |
1 |
|
4 |
|
|
|
1 |
||
5 |
|
|
|
2 |
||
6 |
|
|
|
1 |
1 |
|
7 |
|
|
|
1 |
1 |
|
8 |
|
|
|
1 |
||
9 |
|
|
|
2 |
||
10 |
|
|
|
1 |
1 |
|
The following statements solve the minimization problem:
proc iml;
c = { -6.089 -17.164 -34.054 -5.914 -24.721
-14.986 -24.100 -10.708 -26.662 -22.179 };
start F_BRACK(x) global(c);
s = x[+];
f = sum(x # (c + log(x / s)));
return(f);
finish F_BRACK;
con = { . . . . . . . . . . . . ,
. . . . . . . . . . . . ,
1. 2. 2. . . 1. . . . 1. 0. 2. ,
. . . 1. 2. 1. 1. . . . 0. 1. ,
. . 1. . . . 1. 1. 2. 1. 0. 1. };
con[1,1:10] = 1.e-6;
x0 = j(1,10, .1);
optn = {0 3};
title 'NLPTR subroutine: No Derivatives';
call nlptr(xres,rc,"F_BRACK",x0,optn,con);
The F_BRACK module specifies the objective function, 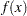 . The matrix CON specifies the constraints. The first row gives the lower bound for each parameter, and to prevent the evaluation of the
. The matrix CON specifies the constraints. The first row gives the lower bound for each parameter, and to prevent the evaluation of the  function for values of
function for values of  that are too small, the lower bounds are set here to 1E
that are too small, the lower bounds are set here to 1E 6. The following three rows contain the three linear equality constraints.
6. The following three rows contain the three linear equality constraints.
The starting point, which must be given to specify the number of parameters, is represented by X0. The first element of the OPTN vector specifies a minimization problem, and the second element specifies the amount of printed output.
The CALL NLPTR statement runs trust-region minimization. In this case, since no analytic derivatives are specified, the F_BRACK module is used to generate finite-difference approximations for the gradient vector and Hessian matrix.
The output is shown in the following figures. The iteration history does not show any problems.
| Optimization Start | |||
|---|---|---|---|
| Active Constraints | 3 | Objective Function | -45.05516448 |
| Max Abs Gradient Element | 4.4710305335 | Radius | 1 |
| Iteration | Restarts | Function Calls |
Active Constraints |
Objective Function |
Objective Function Change |
Max Abs Gradient Element |
Lambda | Trust Region Radius |
||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 2 | 3 | ' | -47.33413 | 2.2790 | 4.3608 | 2.456 | 1.000 | |
| 2 | 0 | 3 | 3 | ' | -47.70050 | 0.3664 | 7.0045 | 0.908 | 0.418 | |
| 3 | 0 | 4 | 3 | -47.73117 | 0.0307 | 5.3051 | 0 | 0.359 | ||
| 4 | 0 | 5 | 3 | -47.73426 | 0.00310 | 3.7015 | 0 | 0.118 | ||
| 5 | 0 | 6 | 3 | -47.73982 | 0.00555 | 2.3054 | 0 | 0.0169 | ||
| 6 | 0 | 7 | 3 | -47.74846 | 0.00864 | 1.3029 | 90.127 | 0.00476 | ||
| 7 | 0 | 9 | 3 | -47.75796 | 0.00950 | 0.5073 | 0 | 0.0134 | ||
| 8 | 0 | 10 | 3 | -47.76094 | 0.00297 | 0.0988 | 0 | 0.0124 | ||
| 9 | 0 | 11 | 3 | -47.76109 | 0.000154 | 0.00447 | 0 | 0.0111 | ||
| 10 | 0 | 12 | 3 | -47.76109 | 3.382E-7 | 9.461E-6 | 0 | 0.00332 |
The output lists the optimal parameters with the gradient.
| Optimization Results | |||
|---|---|---|---|
| Parameter Estimates | |||
| N | Parameter | Estimate | Gradient Objective Function |
| 1 | X1 | 0.040668 | -9.785056 |
| 2 | X2 | 0.147730 | -19.570111 |
| 3 | X3 | 0.783153 | -34.792170 |
| 4 | X4 | 0.001414 | -12.968920 |
| 5 | X5 | 0.485247 | -25.937841 |
| 6 | X6 | 0.000693 | -22.753976 |
| 7 | X7 | 0.027399 | -28.190991 |
| 8 | X8 | 0.017947 | -15.222059 |
| 9 | X9 | 0.037314 | -30.444119 |
| 10 | X10 | 0.096871 | -25.007115 |
The three equality constraints are satisfied at the solution.
| Linear Constraints Evaluated at Solution | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ACT | -1.11E-16 | = | -2.0000 | + | 1.0000 | * | X1 | + | 2.0000 | * | X2 | + | 2.0000 | * | X3 | + | 1.0000 | * | X6 | + | 1.0000 | * | X10 |
| 2 | ACT | -4.406E-16 | = | -1.0000 | + | 1.0000 | * | X4 | + | 2.0000 | * | X5 | + | 1.0000 | * | X6 | + | 1.0000 | * | X7 | ||||
| 3 | ACT | 5.5511E-17 | = | -1.0000 | + | 1.0000 | * | X3 | + | 1.0000 | * | X7 | + | 1.0000 | * | X8 | + | 2.0000 | * | X9 | + | 1.0000 | * | X10 |
The Lagrange multipliers and the projected gradient are also printed. The elements of the projected gradient must be small to satisfy a first-order optimality condition.
Copyright © SAS Institute, Inc. All Rights Reserved.


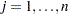



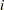 in a molecule of compound
in a molecule of compound